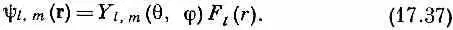Такие амплитуды, как (17.36), встречаются так часто и так важны, что им дали несколько названий. Если амплитуда углового распределения пропорциональна любой из этих трех функций или любой их линейной комбинации, то мы говорим: «орбитальный момент системы равен единице». Или можно сказать: «Ne 20*испускает р -волну». Или говорят: «a-частица испускается в состоянии с l = 1 ». Выражений так много, что даже стоит составить словарик. Если вы хотите понимать разговор физиков, то вам просто нужно выучить их язык. В табл. 17.1 приведен словарь орбитальных моментов количества движения.
Таблица 17.1 · СЛОВАРИК ОРБИТАЛЬНЫХ МОМЕНТОВ ( l = j -ЦЕЛЫЕ ЧИСЛА)
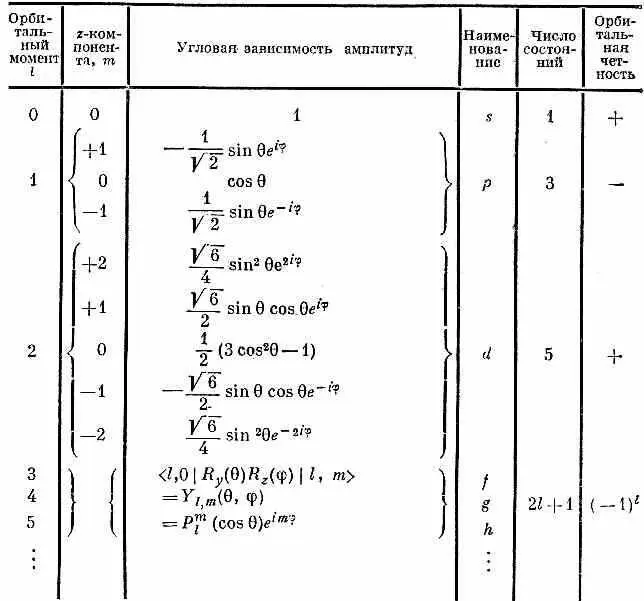
Если орбитальный момент равен нулю, то повороты системы координат ничего не меняют и зависимости от угла нет: «зависимость» от угла имеет вид постоянной, скажем 1. Это называют « s -состоянием». Есть только одно такое состояние, пока дело касается только зависимости от угла. Если орбитальный момент равен 1, то амплитуда зависимости от углов может быть одной из трех приведенных функций, смотря по тому, чему равно m , или их линейной комбинацией. Их называют « р -состояниями».
Таких состояний три. Если орбитальный момент равен 2, то подобных функций пять (см. таблицу). Любая их линейная комбинация называется « l =2»-амплитудой, или амплитудой « d -волны». Теперь вы сразу догадаетесь, какая будет следующая буква. Что должно идти после s, p , d ? Ну, конечно же, f , g , h и т. д. по алфавиту. Буквы эти ничего не значат. [Когда-то они что-то значили: «резкая» (sharp), «главная» (principal), «диффузная» (diffuse) и «фундаментальная» (fundamental) серии линий оптического спектра атомов. Но это было тогда, когда еще не было известно, откуда эти серии линий берутся. После f особых названий уже не было, так что мы сейчас просто продолжаем g , h и т. д.]
Угловые функции в таблице проходят под несколькими именами и определяются порой с небольшими вариациями в численных множителях, стоящих впереди. Иногда их называют «сферические гармоники» и обозначают Y l , m (q,q). Иногда их пишут Р l m (cosq) e im j , а при m = 0 просто Р l (cosq). Функции P l ( cos q) называются «полиномы Лежандра» по cosq, а функции P l m (cosq) именуют «присоединенными функциями Лежандра». Таблицы этих функций встречаются во многих книгах.
Обратите, кстати, внимание, что все функции с данным l имеют одну и ту же четность — при нечетных l они от инверсии меняют свой знак, при четных l — нет. Поэтому можно написать, что четность состояния с орбитальным моментом l равна (-1 ) l .
Как мы видели, одни и те же угловые распределения могут относиться к разным вещам: к ядерному распаду, к другим ядерным процессам, к распределению амплитуд наблюдения электрона в том или ином месте атома водорода. Например, если электрон находится в р -состоянии ( l =1), то амплитуда того, что он обнаружится в каком-то месте, зависит от угла определенным образом, но всегда представляет собой линейную комбинацию трех функций для l = 1 из табл. 17.1. Возьмем очень интересный случай cosq. Он означает, что амплитуда, скажем, положительна в верхней части (q
p/2) и равна нулю при q=90°. Возводя ее в квадрат, видим, что вероятность встретить электрон меняется с q так, как показано на фиг. 17.5, и не зависит от j.
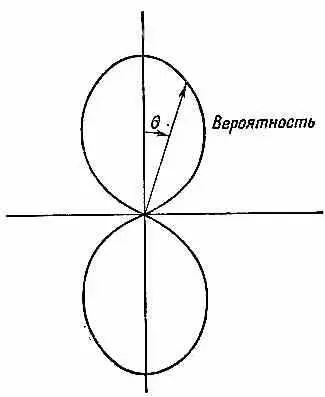
Фиг. 17.5. График cos 2q в полярных координатах, дающий относительную вероятность обнаружения электрона под различными углами к оси z (для данного r ) в состоянии атома с l =1 и m =0.
Такое угловое распределение ответственно за то, что в молекулярной связи притяжение электрона в состоянии l = 1 к другому атому зависит от направления. Отсюда ведет свое начало направленная валентность химического притяжения.
§ 4. Общее решение для водорода
В уравнении (17.35) мы записали волновые функции атома водорода в виде
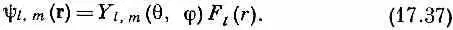
Читать дальше