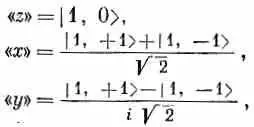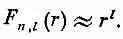Feynmann - Feynmann 9

Имеются и другие s-состояния, с большими энергиями; у них n =2, 3, 4, ... и l = 0 . Каждой энергии соответствует толь­ко одно состояние m = 0 , и все они сферически симметричны. Амплитуды этих состояний с ростом r один или несколько раз меняют знак. Имеется n - 1 сферических узловых поверхностей, или мест, где y проходит через нуль. Например, 2 s -состояние ( l =0, n = 2 ) выглядит так, как показано на фиг. 17.6, б. (Темные области указывают те места, где амплитуда велика, а знаки плюс и минус отмечают относительные фазы амплитуды.) Уровни энергии s-состояний показаны в первом столбце фиг. 17.7.

Фиг. 17.7. Диаграмма уров­ней энергии водорода.

Затем бывают р -состояния с l = 1 . Для каждого n ( n равно или больше 2) существует тройка состояний с одинаковой энергией, одно с m =+1, другое с m =0, третье с m =- 1. Уровни энергии отмечены на фиг. 17.7. Угловые зависимости этих состояний приведены в табл. 17.1. Так, при m = 0 , если амплитуда положи­тельна для углов q, близких к нулю, то при углах q, близких к 180°, она окажется отрицательной. Имеется узловая плос­кость, совпадающая с плоскостью ху. При n >1 бывают также конические узловые по­верхности. Амплитуда n =2, m =0 намечена на фиг. 17.6, в, а волновая функция n =3, m = 0 — на фиг. 17.6, г.

Могло бы показать­ся, что поскольку т дает, так сказать, «ори­ентацию» в простран­стве, то должны наблю­даться еще такие же распределения, но с пи­ками вдоль оси х или вдоль оси у. Можно по­думать, что это скорее всего состояния с m =+1 и с m =-1. Однако это не так! Но зато раз у нас есть тройка состояний с одинаковыми энер­гиями, то любая линейная комбинация из этой тройки тоже будет стационарным состоянием с той же энергией. Оказы­вается, что « x »-состояние (по аналогии с « z »-состоянием, или состоянием с m =0, см. фиг. 17.6, в) это линейная комбинация состояний с m =+1' и с m =-1. Другая комбинация дает « y »-состояние. Точнее, имеется в виду, что состояния

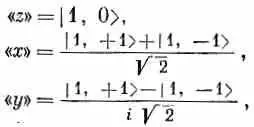
если отнести их к своим осям, выглядят одинаково.

У d-состояний ( l =2) для каждой энергии есть пять возмож­ных значений т; наинизшей энергией обладает n =3. Уровни показаны на фиг. 17.7. Угловые зависимости усложняются. К примеру, состояния с m =0 обладают двумя коническими узловыми поверхностями, так что при переходе от северного по­люса к южному волновая функция меняет фазы с + на — и обратно на +. Примерная форма амплитуды нарисована на фиг. 17.6, д и е для состояний с m =0 и n =3 и 4. И снова при больших n появляются конические узловые поверхности.

Мы не будем пытаться описывать другие последующие со­стояния. Подробное изложение волновых функций водорода вы найдете во многих книгах. Рекомендую вам особенно; L. Pauling, E.B.Wilson, Introduction to Quantum Mechanics, New York, 1935; R. B. Leightоn. Principles of Modern Physics, New York, 1959. В этих книгах вы найдете графики некоторых функций и графическое изображение многих со­стояний.

Хотелось бы упомянуть об одном особом свойстве волновых функций при высших l : при l >0 амплитуды обращаются в центре в нуль. Ничего в этом удивительного нет, ведь электрону трудно иметь большой момент, когда плечо момента очень мало. По этой причине чем l большe, тем дальше амплиту­ды «отталкиваются» от центра. Если вы посмот­рите, как радиальные функции F ( r ) меняются при малых r , то из (17.53) окажется, что

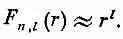
Такая зависимость от r означает, что при боль­ших l вам придется даль­ше отойти от r =0, чтобы получить заметную ампли­туду. Такое поведение, кстати, определяется чле­ном с центробежной силой в радиальном уравнении, так что все это применимо к любому потенциалу, который при малых r меняется медленнее, чем 1/r 2, а таково большинство атомных потенциалов.

§ 6. Периодическая таблица

Теперь мы хотели бы применить теорию атома водорода к объяснению химической периодической таблицы элементов. В атоме элемента с атомным номером Z имеется Z электронов, которые удерживаются электрическим притяжением ядра, но при этом взаимно отталкиваются друг от друга. Чтобы полу­чить точное решение, пришлось бы решить уравнение Шредин­гера для Z электронов в кулоновом поле. Для гелия уравнение имеет вид