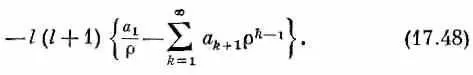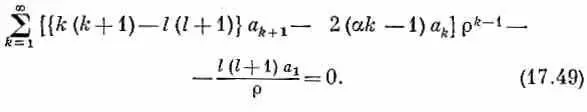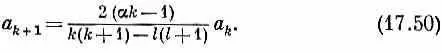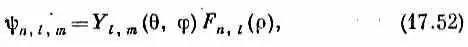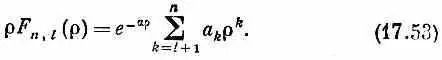Feynmann - Feynmann 9

Теперь мы уже можем решить уравнение (17.46) относительно F l ( r ). Оно очень похоже на (17.8), так что прибегнем к той же технике. Все повторяется вплоть до уравнения (17.19), в кото­ром появится добавочный член

Его можно записать еще и так:

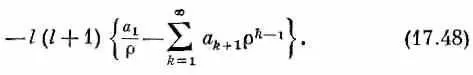
(Мы выделили первый член, а затем текущий индекс k сдвинули на единицу.) Вместо (17.20) появится

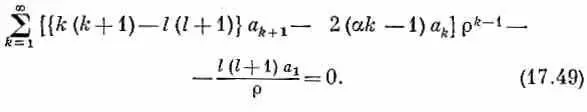
Поскольку член с r -1только один, то он должен обратиться в нуль. Коэффициент a 1 должен быть равен нулю (если только l не равно нулю, но тогда мы приходим к нашему прежнему реше­нию). А когда все квадратные скобки при любых k обратятся в нуль, то и все следующие члены станут равны нулю. Из-за этого условие (17.21) переходит в

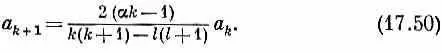
Это единственное существенное видоизменение по сравнению со сферически симметричным случаем.

Как и раньше, ряд должен оборваться, если мы хотим, чтобы решения представляли связанные электроны. Если a n =1, то ряд оборвется на k = n . Условие на а получается таким же: а должно быть равно 1/ n , где n — целое число. Однако (17.50) приводит и к новому ограничению. Индекс k не может быть равен l , в противном случае знаменатель обратится в нуль, а а l + 1 — в бесконечность. Иначе говоря, поскольку a 1=0, то (17.50) подразумевает, что все последовательные a k обращаются в нуль, пока мы не придем к а l +1, которое может быть и не ну­лем. Это означает, что k должно начинаться с l +1 и кончаться

на п.

Окончательный итог таков: при любом l имеется набор возможных решений, которые мы обозначим F n , l , где n > l +1. Каждое решение обладает энергией

Волновая функция состояния с такой энергией и с угло­выми квантовыми числами l и m имеет вид

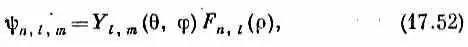
где

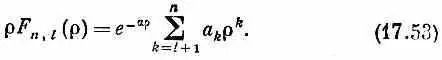
Коэффициенты a kполучаются из (17.50). Наконец-то в наших руках полное описание состояний атома водорода.

§ 5. Волновые функции водорода

Посмотрим же, что мы открыли. Состояния, которые удов­летворяют уравнению Шредингера для электрона в кулоновом поле, характеризуются тремя (причем целыми) квантовыми числами n , l , m . Угловое распределение амплитуды электрона может обладать только определенными формами, которые мы обозначим Y l , m . Они нумеруются числом l — квантовым числом полного момента количества движения я т — «магнитным» квантовым числом, которое может меняться от - l до + l . При каждой угловой конфигурации возможны различные радиаль­ные распределения F n , l (r) амплитуды электрона; они нумеруют­ся главным квантовым числом n , которое может меняться от l +1 до Ґ . Энергия состояния зависит только от n и растет с n . Состояние наинизшей энергии, или основное, является s -состоянием. У него l = 0 , n =1 и m = 0 . Это «невырожденное» состояние: имеется только одно состояние с такой энергией, а волновая функция у него сферически симметрична. Амплитуда того, что электрон обнаружится, достигает максимума в центре и монотонно спадает с удалением от центра. Эту электронную амплитуду можно изобразить этаким комочком (фиг. 17.6, а ).

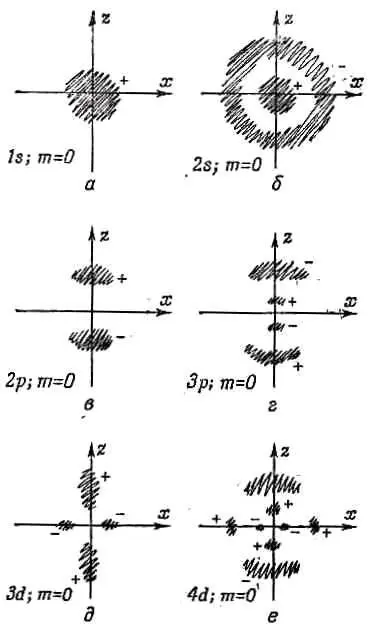
Фиг. 17.6. Наброски, отражающие общий харак­тер волновых функций водорода.

В заштрихованных местах ам­плитуды велики. Знаки плюс и минус — это относительные знаки амплитуд в каждой об­ласти.