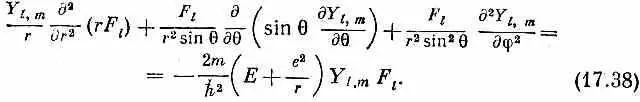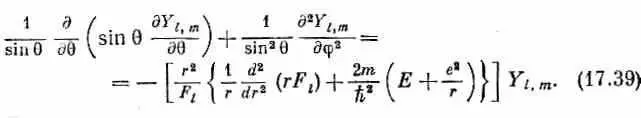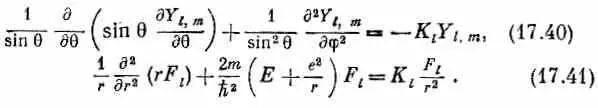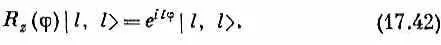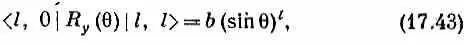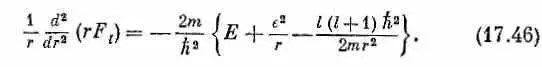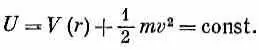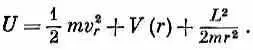Feynmann - Feynmann 9

Эти волновые функции должны быть решениями дифференци­ального уравнения (17.7). Посмотрим, что это означает. Под­ставим (17.37) в (17.7); получим

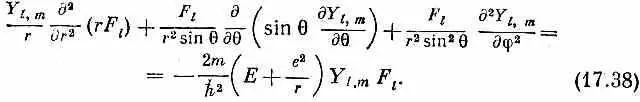
Помножим все на r 2 / F l и переставим члены; результат будет таков:

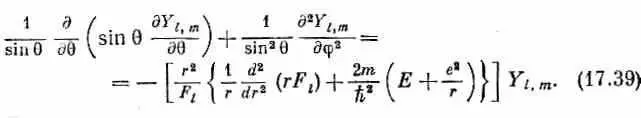
Левая часть этого уравнения зависит от q и j, а от r не зависит. Какое бы значение r мы ни взяли, от этого левая часть не изме­нится. Значит, то же должно быть выполнено и для правой части. Хотя в выражении в квадратных скобках там и сям попадаются разные r , все выражение от r зависеть не может, иначе бы не получилось уравнение, которое годится для всех r . Кроме того, как вы видите, эта скобка не зависит ни от q, ни от j. Она должна быть постоянным числом. Его величина имеет право зато зави­сеть от значения l того состояния, которое мы изучаем, поскольку этому состоянию принадлежит функция F l ; поэтому постоянное число мы обозначим K l . Уравнение (17.35), стало быть, равно­значно двум уравнениям

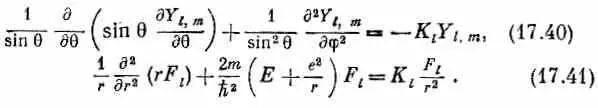
Теперь взглянем на то, что мы сделали. Для каждого состоя­ния, описываемого числами l и m , мы знаем функции Y l , m ; тогда из уравнения (17.40) можно определить K l Затем, подставив K l в (17.41), мы получим дифференциальное уравнение для функции F l ( r ). Если мы его сможем решить, то все множители, входящие в (17.37), нам станут известны, и мы узнаем y(r).

Чему же равно К l ? Ну, во-первых, заметьте, что при всех т (входящих в данное l ) оно должно быть одним и тем же, поэтому мы вправе выбрать в Y l , m то m , какое нам нравится, и вставить его в (17.40). Пожалуй, проще всего взять Y l,l . Из уравнения (16.24)

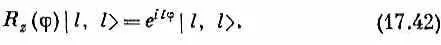
Матричный элемент R y (q) тоже совсем прост:

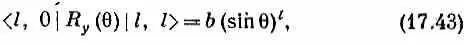
где b — некоторое число. Объединяя их, получаем

Подстановка этой функции в (17.40) даст

Теперь, когда мы определили К l , уравнение (17.41) даст нам радиальную функцию F l ( r ). Перед нами обычное уравнение Шредингера, у которого угловая часть заменена ее эквивален­том K l F l / r 2 . Перепишем (17.41) в той форме, в какой мы писали уравнение (17.8):

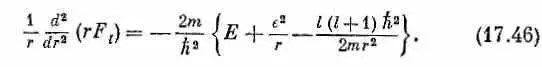
У потенциальной энергии появилась какая-то таинственная добавка. Хотя она появилась на свет после длинной серии мате­матических шагов, тем не менее у нее простое физическое проис­хождение. Мы беремся рассказать о ее происхождении при помощи полуклассических аргументов. После этого она уже не покажется вам такой таинственной.

Представим классическую частицу, вращающуюся вокруг некоторого силового центра. Полная энергия сохраняется и является суммой потенциальной и кинетической энергий

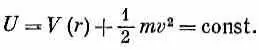
В общем случае v разлагается на радиальную компоненту v r и на касательную компоненту r q, т. е.

v 2 = v 2 r + ( r q) 2.

Момент количества движения mr 2 q тоже сохраняется; пусть он равняется L . Тогда можно написать

mr 2q= L, или r q = L/mr ,

т. е. энергия равна

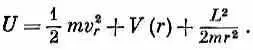
Если бы момента количества движения не было, у нас осталось бы только два первых члена. Добавление момента количества движения L изменяет энергию как раз так, как если бы к потен­циальной энергии добавился член L 2 / 2 mr 2 . Но он почти точно совпадает с добавкой (17.46). Единственная разница в том, что вместо ожидаемого числителя l 2 h 2(этого можно было бы ожидать) появляется комбинация l ( l +1) h 2Но мы еще раньше видели [например, в гл. 34, § 7 (вып. 7)], что это обычная замена, к которой всегда приходится прибегать, если хотят, чтобы квази­классические рассуждения совпали с правильным квантовомеханическим расчетом. Поэтому новый член можно понимать как своего рода «потенциал», определяющий «центробежную силу» и возникающий в уравнениях радиального движения вращаю­щейся системы [см. гл. 12, § 5 (вып. 1)].