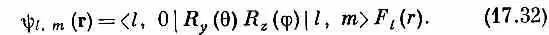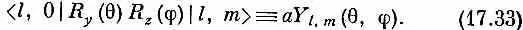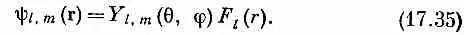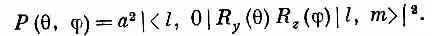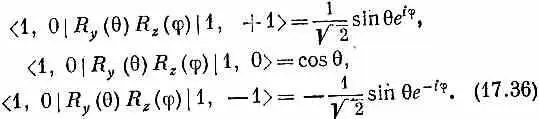Feynmann - Feynmann 9

В итоге получаем

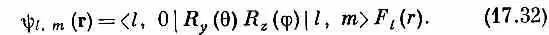
Орбитальное движение может обладать только целыми зна­чениями l . (Если электрон может быть обнаружен в любом месте, где r № 0 , то имеется некоторая амплитуда того, что в этом на­правлении будет m =0. А состояния с m =0 бывают только при целых спинах.) Матрицы поворота для l =1 приведены в табл.15.2 (стр. 129). Для больших l вы можете воспользоваться общими формулами, выведенными в гл. 16. Матрицы R z (j) и R y (q) написаны по отдельности, но как их комбинировать, вы знаете. В общем случае вы начнете с состояния | l , m > и подей­ствуете на него оператором R z (j), получив новое состояние R z (j)| l , т > (которое просто равно e im j | l , m > ) . Затем вы подействуете на это состояние оператором R y (q) и получите состояние R y (q) R z (j) | l , m >. Умножение на < l , 0| даст вам матричный элемент (17.31).

Матричные элементы операции поворота — это алгебраиче­ские функции от q и j. Те частные виды функций, которые появляются в (17.31), возникают и во многих других задачах, связанных с волнами на сфере. Им присвоили особое имя. Правда, не у всех авторов обозначения одинаковы; чаще всего все же пишут

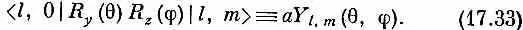
Функции Y l , m (q, j) называют сферическими гармониками, a a — просто численный множитель, который зависит от того, как определено Y l , m . При обычном определении

В этих обозначениях волновые функции водорода записываются так:

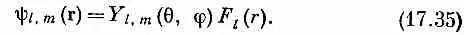
Угловые функции Y l , m (q,j) важны не только во многих квантовомеханических задачах, но и во многих областях клас­сической физики, в которых встречается оператор С 2, например в электромагнетизме. В качестве другого примера их примене­ния в квантовой механике рассмотрим распад возбужденного состояния Ne 20(о котором говорилось в предыдущей главе), которое испускает a-частицу и превращается в О 16:

Neao'^o^-fHe 4.

Допустим, что возбужденное состояние имеет спин l (обяза­тельно целый), а z -компонента момента количества движения есть т. Спросим вот о чем: если даны l и т, то какова амплитуда того, что a-частица вылетит в направлении, составляющем с осью z угол q и с плоскостью xz угол j (фиг. 17.4)?

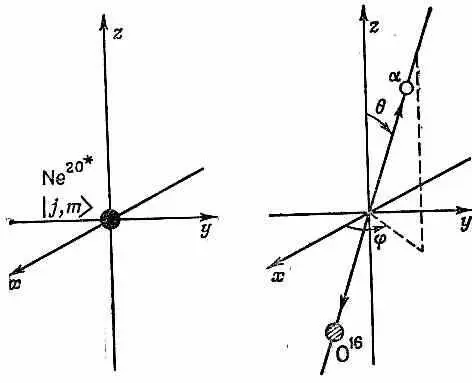
Фиг. 17.4. Распад возбужденного состояния Ne 20.

Решить эту задачу нам поможет следующее наблюдение. Распад, в котором a-частица вылетает прямо вдоль оси z, должен происходить из состояния с m = 0 . Это потому, что у самих О 16 и a-частицы спин равен нулю, а за счет движения вдоль оси z момента вокруг этой оси не создашь. Обозначим эту амплитуду а (на единицу телесного угла). Тогда, чтобы найти амплитуду распада под произвольным углом (см. фиг. 17.4), остается только узнать, с какой амплитудой данное начальное состояние будет обладать нулевым моментом относительно направления распада. Амплитуда того, что распад будет в направлении (q, j), тогда будет равна произведению а на амплитуду того, что состояние | l , т > относительно оси z окажется в состоянии | l , 0> отно­сительно z ' (направления распада). Эта последняя амплитуда как раз и есть то, что мы писали в (17.31). Вероятность увидеть a-частицу под углом (q, j), стало быть, равна

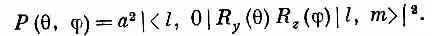
Для примера рассмотрим начальное состояние с l =1 и различными т. Из табл. 15.2 (стр. 129) мы знаем все нужные амплитуды:

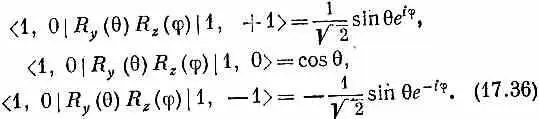
Это и есть три возможные амплитуды угловых распределений, в зависимости от того, какое т у первоначального ядра.