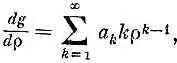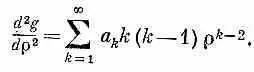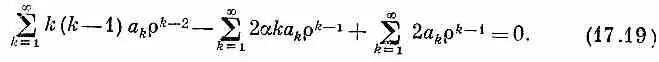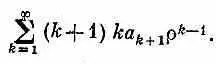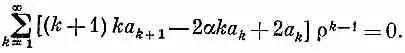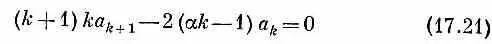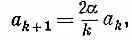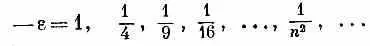где a k— постоянные коэффициенты. И нам осталось только найти подходящую бесконечную последовательность коэффициентов! Проверим, годится ли такая запись решения, Первая производная такой функции g (r) равна
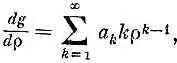
а вторая
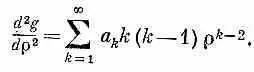
Подставляя это в (17:17), имеем
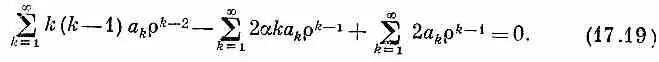
Пока еще не ясно, вышло ли у нас что-нибудь; но мы рвемся вперед. Если мы первую сумму заменим некоторым ее эквивалентом, то все выражение станет выглядеть лучше. Первый член в сумме равен нулю, поэтому каждое k можно заменить на k +1, от этого ничего в бесконечном ряде не изменится. Значит, первую сумму мы вправе записать и так:
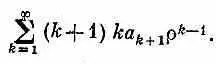
Теперь можно объединить все три суммы в одну:
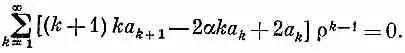
Этот степенной ряд должен обращаться в нуль при всех мыслимых значениях r, что возможно лишь тогда, когда коэффициенты при каждой степени r порознь равны нулю. Мы получим решение для атома водорода, если отыщем такую последовательность a k , для которой
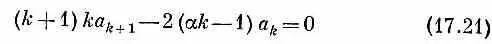
при всех k >1. А это, конечно, устроить легко. Выберите какое угодно а 1 . Затем все прочие коэффициенты образуйте с помощью формулы

Пользуясь ею, вы получите а 2, а 3, а 4и т. д., и каждая пара будет, конечно, удовлетворять (17.21). Мы получим ряд для g (r), удовлетворяющий (17.17). С его помощью мы напишем y — решение уравнения Шредингера. Обратите внимание, что решения зависят от того, какова предполагаемая энергия (через a), но для каждого значения e получается свой ряд. Решение-то у нас есть, но что оно представляет физически? Понятие об этом мы получим, поглядев, что происходит вдалеке от протона — при больших r. Там основное значение приобретают наивысшие степени членов ряда, т. е. нам надо посмотреть, что бывает при больших k . Когда k>>1, то уравнение (17.22) приближенно совпадает с :
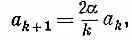
а это означает, что

Но это как раз коэффициенты разложения в ряд е +2 a r. Функция g оказывается быстро растущей экспонентой. Даже после умножения на е - a r получающаяся функция f (r) [см. (17.14)] будет при больших r меняться как е a r. Мы нашли математическое решение, но оно не является физическим. Оно представляет случай, когда электрону менее всего вероятно очутиться вблизи протона! Чаще всего он вам повстречается на очень больших расстояниях р. А волновая функция для связанного электрона должна при больших r стремиться к нулю.
Придется подумать, нельзя ли как-нибудь обмануть решение. Оказывается, можно. Посмотрите! Если бы, по счастью, оказалось, что a = 1 / n , где n — любое целое число, то уравнение (17.22) привело бы к a n + 1=0. И все высшие члены обратились бы тоже в нуль. Вышел бы не бесконечный ряд, а конечный многочлен. Любой многочлен растет медленнее, чем е a r, поэтому множитель е - aнаверняка забьет его при больших r, и функция f при больших r будет стремиться к нулю. Единственные решения для связанных состояний это те, для которых a=1/n, где n =1, 2, 3, 4 и т. д.
Оглядываясь на уравнение (17.16), мы видим, что у сферически симметричного волнового уравнения могут существовать решения для связанных состояний лишь при энергиях
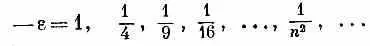
Читать дальше