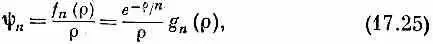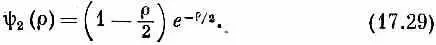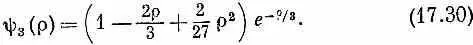Feynmann - Feynmann 9

Допустимы только те энергии, которые составляют именно такую часть ридберга Е R = me 4 /2 h 2 , т. е. энергия n -го уровня равна

Кстати, ничего мистического в отрицательных энергиях нет. Они отрицательны просто потому, что когда мы решили писать V = - е 2 / r , то тем самым в качестве нуля энергии выбрали энергию электрона, расположенного вдалеке от протона. Когда он ближе, то его энергия меньше, т. е. ниже нуля. Энергия ни­же всего (самая отрицательная) при n =1 и возрастает к нулю с ростом п.

Еще до открытия квантовой механики экспериментальное изучение спектра водорода показало, что уровни энергии описы­ваются формулой (17.24), где Е R , как это следует из измерений, равно примерно 13,6 зв. Затем Бор придумал модель, которая привела к тому же уравнению (17.24) и предсказала, что E R должно равняться me 4 / 2 h 2 . Первым большим успехом теории Шредингера явилось то, что она смогла воспроизвести этот результат прямо из основного уравнения движения электрона.

Теперь, когда мы рассчитали наш первый атом, давайте рас­смотрим свойства полученного нами решения. Объединим все выделившиеся по дороге факторы и выпишем окончательный вид решения:

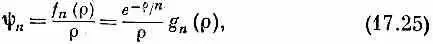
где

и

Пока нас интересует главным образом относительная вероят­ность обнаружить электрон в том или ином месте, можно в ка­честве а 1 выбирать любое число. Возьмем, например, а 1=1 . (Обычно выбирают а 1 так, чтобы волновая функция была «нор­мирована», т. е. чтобы полная вероятность обнаружить элек­трон где бы то ни было в атоме была равна единице. Мы в этом сейчас не нуждаемся.)

В низшем энергетическом состоянии n =1 и

Если атом водорода находится в своем основном (наиболее низ­ком энергетическом) состоянии, то амплитуда того, что элект­рон будет обнаружен в каком-то месте, экспоненциально падает с расстоянием от протона. Вероятнее всего встретить его вплотную близ протона. Характерное расстояние, на котором он встречается, составляет около одного r, или одного боровского радиуса r B .

Подстановка n =2 дает следующий более высокий уровень. В волновую функцию этого состояния входят два слагаемых. Она равна

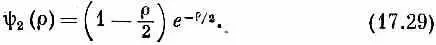
Волновая функция для следующего уровня равна

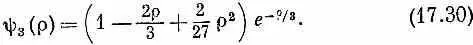
Эти три волновые функции начерчены на фиг. 17.2.

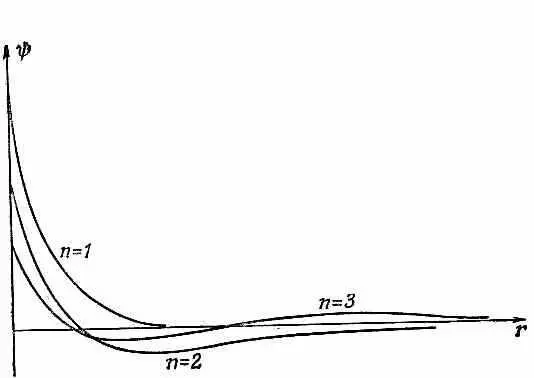
Фиг. 17.2. Волновые функции трех первых состоя­ний атома водорода с l =0. Масштабы выбраны так, чтобы полные вероятности совпадали.

Общая тен­денция уже видна. Все волновые функции при больших r, поко­лебавшись несколько раз, приближаются к нулю. И действи­тельно, число «изгибов» у y n как раз равно n , или, если угодно, число пересечений оси абсцисс — число нулей — равно n - 1.

§ 3. Состояния с угловой зависимостью

Мы нашли, что в состояниях, описываемых волновой функ­цией y n ( r ) , амплитуда вероятности обнаружить электрон сфе­рически симметрична; она зависит только от r — расстояния до протона. Момент количества движения таких состояний равен нулю. Теперь займемся состояниями, у которых какой-то момент количества движения имеется.

Можно было бы, конечно, просто исследовать чисто матема­тическую задачу отыскания функций от r, q и j, удовлетворяю­щих дифференциальному уравнению (17.7), добавив только физическое условие, что единственно приемлемые для нас функции — это такие, которые при больших r стремятся к нулю. Так почти всегда и поступают. Но мы попробуем несколько сократить наш путь и воспользоваться тем, что мы уже знаем, именно тем, что нам известно, как амплитуды зависят от про­странственных углов.