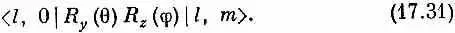Атом водорода в том или ином состоянии — это частица с определенным «спином» j — квантовым числом полного момента количества движения. Часть этого спина возникает от собственного спина электрона, другая — от движения электрона. Поскольку каждая из этих частей действует (в очень хорошем приближении) независимо, то мы по-прежнему будем игнорировать спиновую часть и учтем только «орбитальный» момент. Впрочем, это орбитальное движение в точности подобно спину. Скажем, если орбитальное квантовое число есть l , то z -компонента момента количества движения может быть l , l - 1, l -2, . . ., - l . (Мы, как обычно, измеряем все в единицах h .) Кроме того, по-прежнему годятся все наши матрицы поворота и прочие известные свойства. (Начиная с этого места, мы действительно начнем пренебрегать спином электрона; говоря о «моменте количества движения», мы будем иметь в виду только орбитальную его часть.)
Поскольку поле с потенциалом V , в котором движется электрон, зависит только от r , а не от q и не от j, то гамильтониан симметричен относительно поворотов. Отсюда следует, что и момент количества движения и все его проекции сохраняются. Это не есть особое свойство кулонова потенциала e 2 / r ; оно справедливо при движении в любом «центральном поле» — поле, зависящем только от r .
Представим себе некоторое возможное состояние электрона; внутренняя угловая структура этого состояния будет определяться квантовым числом l . В зависимости от «ориентации» полного момента количества движения относительно оси z его проекция т на ось z может равняться одному из 2 l +1 чисел между + l и - l . Пусть, например, m =1. С какой амплитудой электрон окажется на оси z на расстоянии r от начала? С нулевой. Электрон на оси z не может иметь какого-либо орбитального момента относительно этой оси. Но пусть тогда m =0. Вот это другое дело; теперь уже может появиться не равная нулю амплитуда того, что электрон окажется на оси z на таком-то расстоянии от протона. Обозначим эту амплитуду F l ( r ). Это — амплитуда того, что электрон будет обнаружен на расстоянии r по оси z, когда атом находится в состоянии | l , 0>, т. е. в состоянии с орбитальным моментом l и его z -компонентой m =0. А если нам известно F l ( r ), то известно все. Теперь уже в любом состоянии | l , m > мы можем узнать амплитуду y lm ( r ) того, что электрон обнаружится в произвольном месте атома. Как мы это узнаем? А вот следите. Пусть у нас есть атом в состоянии | l , m > . Какова амплитуда того, что электрон обнаружится под углом q, j и на расстоянии r от начала? Проведите новую ось z, скажем z', под этим углом (фиг. 17.3) и задайте вопрос: какова амплитуда того, что электрон окажется на новой оси z на расстоянии r ?
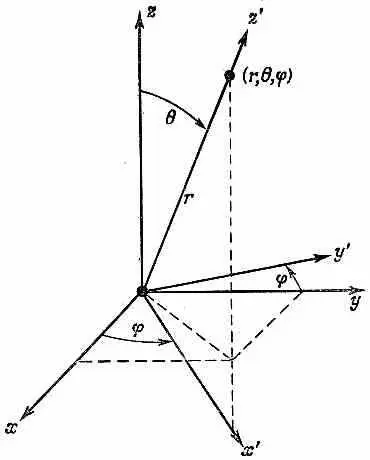
Фиг. 17.3. Точка (х, у, z ) лежит на оси z ' системы координат х ' , у', z '.
Мы знаем, что он не сможет оказаться на оси z', если только m — его z'-компонента момента количества движения — не равна нулю. Когда же m ' =0, то амплитуда того, что электрон обнаружится на оси z ', есть F l ( r ). Значит, результат получится перемножением двух амплитуд. Первая это амплитуда того, что атом, находящийся в состоянии | l , т > относительно оси z, окажется в состоянии | l , m '= 0> относительно оси z ' . Умножьте эту амплитуду на F l ( r ) и вы получите амплитуду y l , m( r) того, что электрон обнаружится в точке ( r , q, j) относительно первоначальной системы осей.
Давайте все это распишем. Матрицы преобразования для поворотов мы уже вычислили. Чтобы перейти от системы х, у, z к системе х', у', z ' (см. фиг. 17.3), можно сперва сделать поворот вокруг оси z на угол j, а потом сделать поворот вокруг новой оси у (оси у') на угол q. Совместный поворот выразится произведением
R у (q) R z (j).
Амплитуда того, что после поворота обнаружится состояние | l , m ' =0>, есть
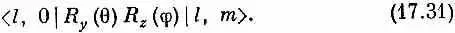
Читать дальше