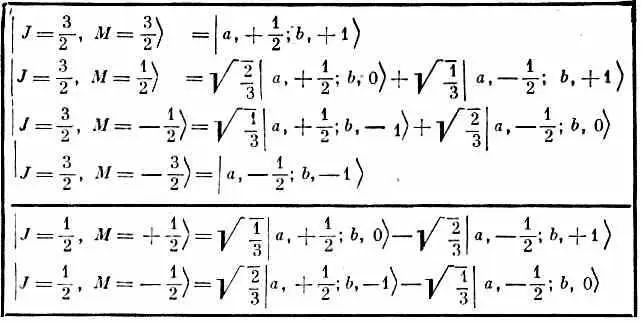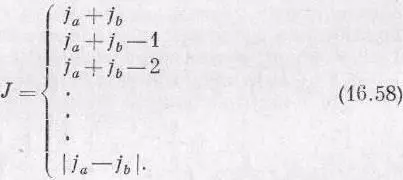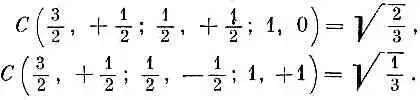Feynmann - Feynmann 9

Таблица 16.6 · ОБЪЕДИНЕНИЕ ЧАСТИЦЫ СО СПИНОМ 1/ 2( j a= 1/ 2) С ЧАСТИЦЕЙ СО СПИНОМ 1 ( j b =1)

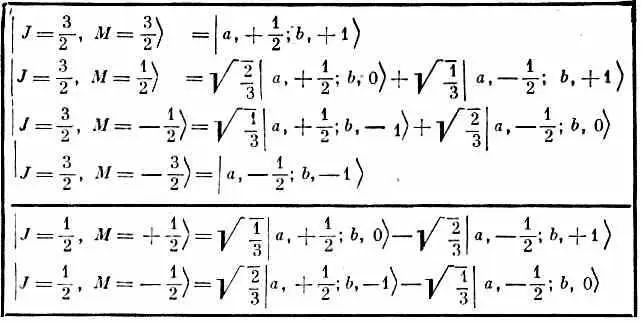
Поставим теперь себе общую задачу найти состояния, кото­рые можно образовать, объединяя два объекта с произвольными спинами. Скажем, у одного спин j a (так что его z -компонента m а пробегает 2 j а +1 значений от - j a до + j a , а у другого j b (с z-компонентой m b , пробегающей значения от - j b до+ j b ).

Объединенные состояния суть | а, m а ; b , m b > , их всего (2 j a +1)(2 j b +1). Какие же состояния с полным спином / мы обнаружим?

Полная z-компонента М момента количества движения рав­няется m а + m b , и все состояния можно перечислить, опираясь на величину М [как в (16.42)]. Наибольшое М является единст­венным; оно отвечает значениям m a = j a и m b = j b и равно по­просту j a + j b . Это означает, что наибольший полный спин J также равен сумме j а + j b :

J = М макс= j a + j b .

Следующему значению М, меньшему чем М максна единицу, будут соответствовать два состояния (либо m а , либо m b меньше своих максимальных значений на единицу). Из них должно быть образовано одно состояние, принадлежащее совокупности с J = j a + j b , и останется еще одно, которое будет принадлежать новой совокупности с J = j a + j b - 1. Следующее значение М (третье сверху) можно составить тремя путями (из m a = j a — 2, m b = j b , из m a = j a - 1, m b = j b - 1 и из m a = j a , m b = j b - 2). Два из них принадлежат к уже начавшим составляться груп­пам; третье говорит нам, что надо включить в рассмотрение и со­стояния с J = j a + j b -2. Такие рассуждения будут продол­жаться до тех пор, пока уже нельзя будет, меняя то одно, то дру­гое т, получать новые состояния.

Пусть из j а и j b меньшим является j b (а если они одинаковы, возьмите любое из них); тогда понадобятся только 2 j b значений полного спина J , идущих единичными шагами от j а + j b вниз к j а - j b . Иначе говоря, когда объединяются два объекта со спинами j а и j b , то полный момент количества движения J их системы может равняться одному из значений:

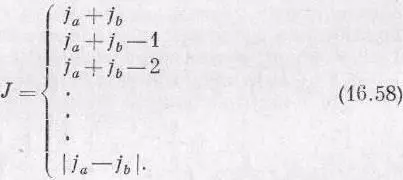
(Написав | j a - j b | вместо j a - j b , мы можем избежать напо­минания о том, что j a і j b .)

Для каждого из этих значений J имеется 2J+1 состояний с различными значениями М; М меняется от + J до - J . Каждое из них образовано из линейных комбинаций исходных состояний | а, m а ; b , m b > с соответствующими коэффициентами — коэффициентами Клебша — Гордона для каждого отдельного члена. Можно считать, что эти коэффициенты дают «количест­во» состояния | j a , m a ; j b , m b > , проявляющегося в состоянии

Таблица 16.7 · ОБЪЕДИНЕНИЕ ДВУХ ЧАСТИЦ СО СПИНОМ 1 ( j a =1, j b =1)

I /, My . Так что каждый из коэффициентов Клебша — Гордона обладает, если угодно, шестью индексами, указывающими его положение в формулах типа приведенных в табл. 16.3 и 16.6. Иначе говоря, обозначая, скажем, эти коэффициенты С ( J , М; j a , m a ; j b , m b ), можно выразить равенство во второй строчке табл. 16.6 так:

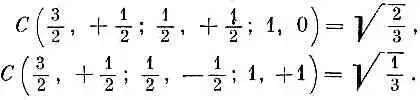
Мы не будем здесь подсчитывать коэффициенты для других частных случаев. Но вы обнаружите такие таблицы во мно­гих книжках. Попробуйте сами подсчитать другой случай, например объединение двух объектов со спином 1. Мы же про­сто привели в табл. 16.7 окончательный результат.