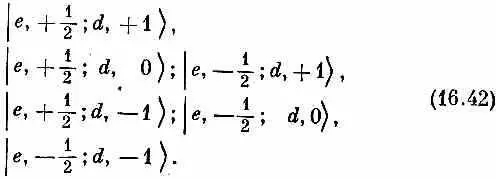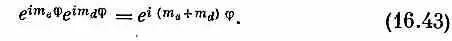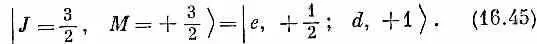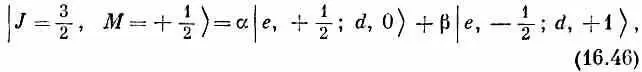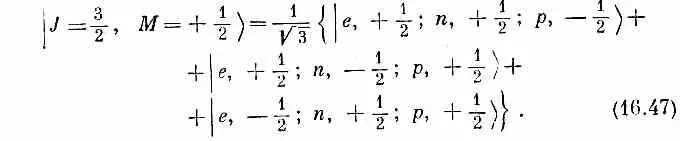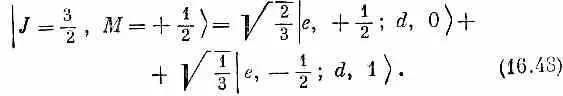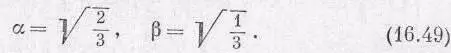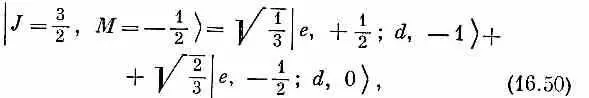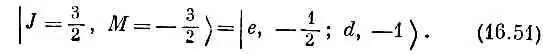Feynmann - Feynmann 9

| е, m e ; d, m d >):

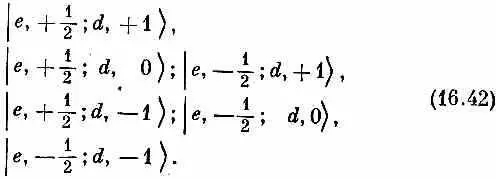
Обратите внимание, что мы разверстали состояния согласно значениям суммы m e и m d в порядке ее убывания.

Спросим теперь: что случится с этими состояниями, если спроецировать их в другую систему координат? Если эту новую систему просто повернуть вокруг оси z на угол j, то состояние | е, m e ; d , m d > умножается на

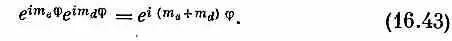
(Состояние можно считать произведением | е, m е >| d , m d >, и каждый вектор состояния независимо привнесет свой собст­венный экспоненциальный множитель.) Множитель (16.43) имеет форму е iM j , поэтому z-компонента момента количества движения у состояния | е, m е ; d , m d > окажется равной

M = m e + m d . (16.44)

Иначе говоря, z -компонента полного момента количества движения есть сумма z -компонент моментов количества движе­ния отдельных частей.

Значит, в перечне состояний (16.42) верхнее состояние имеет М =+ 3/ 2, Два следующих М =+ 1/ 2, затем два М =- 1/ 2 и последнее состояние М= - 3/ 2. Мы сразу же видим, что одной из возможностей для спина J объединенного состояния (для полного момента количества движения) должно быть 3/ 2, это потребует четырех состояний с М = + 3/ 2, + 1/ 2 , - 1/ 2и - 3/ 2. На М= + 3/ 2есть только один кандидат, и мы сразу видим, что

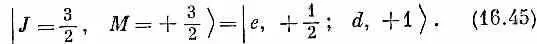
Но что является состоянием | J = 3/ 2, М =+ 1/ 2>? Кандидатов здесь два, они стоят во второй строчке (16.42), и всякая их ли­нейная комбинация тоже даст М= + 1/ 2 . Значит, в общем случае можно ожидать, что

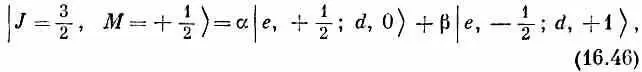
где a и b — два числа. Их именуют коэффициенты Клебша — Гордона. Найти их и будет нашей очередной задачей.

И мы их легко найдем, если просто вспомним, что дейтрон состоит из нейтрона и протона, и в явном виде распишем со­стояния дейтрона, пользуясь правилами табл. 16.3. Если это проделать, то перечисленные в (16.42) состояния будут выгля­деть так, как показано в табл. 16.4.

Пользуясь состояниями из этой таблицы, мы хотим образо­вать четверку состояний с J = 3/ 2. Но ответ нам уже известен, потому что в табл. 16.1 уже стоят состояния со спином 3/ 2, образованные из трех частиц со спином 1/ 2. Первое состояние в табл. 16.1 имеет | J = 3/ 2, М =+ 3/ 2>, это |+++>, а в наших нынешних обозначениях это | e , + 1/ 2; n , + 1/ 2; p , + 1/ 2>, или первое состояние из табл. 16.4. Но это состояние — то же самое, что первое по списку в (16.42), так что наше выражение (16.45) подтверждается. Вторая строчка в табл. 16.1 утверждает, если воспользоваться нашими теперешними обозначениями, что

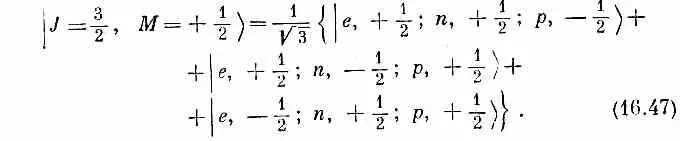
То, что стоит в правой части, можно, очевидно, составить из двух членов во второй строчке табл. 16.4, взяв Ц 2/ 3от пер­вого члена и Ц 1/ 3 от второго. Иначе говоря, (16.47) эквива­лентно

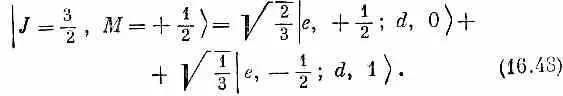
Таблица 16.4 · СОСТОЯНИЯ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ АТОМА ДЕЙТЕРИЯ

Мы нашли два наших первых коэффициента Клебша — Гор­дона a , и b [см. (16.46)]:

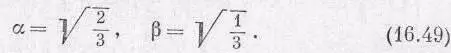
Повторяя ту же процедуру, найдем

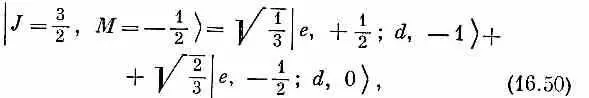
а также, конечно,

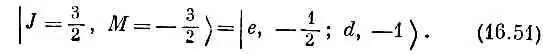
Это и есть правила составления из спина 1 и спина 1/ 2полного спина J = 3/ 2. Мы свели (16.45) и (16.50) в табл. 16.5.