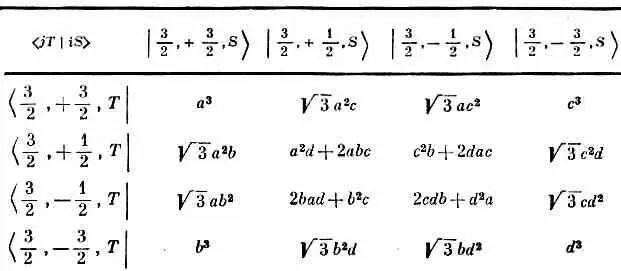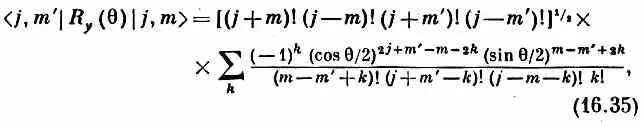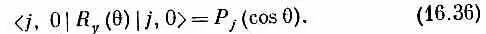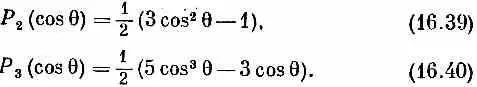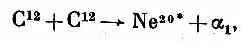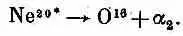Feynmann - Feynmann 9

Таблица 16.2 · МАТРИЦА ПОВОРОТА ДЛЯ ЧАСТИЦЫ СО СПИНОМ 3/ 2

Коэффициенты а, b , с и d объясняются в табл. 10.4.

Рассуждения, которые мы только что провели, были обобще­ны на систему с произвольным спином j . Состояния | j , m > можно составить из 2 j частиц со спином 1/ 2у каждой. (Из них j + m будут в ] + >-состоянии, а j - m будут в |->-состоянии.) Проводится суммирование по всем возможным способам, какими их можно сочетать, а затем состояния нормируются умноже­нием на надлежащую постоянную. Если у вас есть способности к математике, то вы сможете доказать, что получается следую­щий результат:

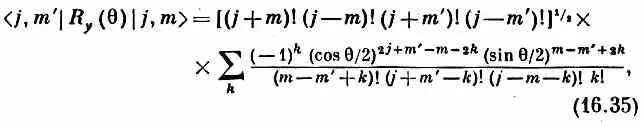
где k пробегает все те значения, при которых под знаком факториала получаются неотрицательные величины.

Это очень запутанная формула, но с ее помощью вы сможете проверить табл. 15.2 для j =1 (стр. 129) и составить ваши собственные таблицы для больших j . Некоторые матричные элементы очень важны и получили особые наименования. Например, матричные элементы для m = m '= 0 и целых j известны под названием полиномов Лежандра и обозначаются </, 0 |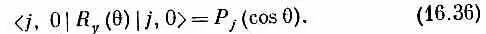

Первые из них таковы:

P 0(cosq)=l, (16.37)

P 1(cosq)=cosq, (16.38)

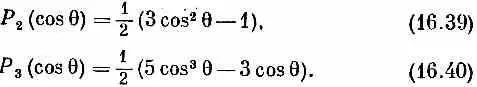
§ 5. Измерение ядерного спина

Продемонстрируем теперь пример, где понадобятся только что описанные коэффициенты. Он связан с проделанными не так давно интересными опытами, которые вы теперь в состоянии будете понять. Некоторым физикам захотелось узнать спин одного из возбужденных состояний ядра Ne 20. Для этого они принялись бомбить углеродную мишень пучком ускоренных ионов углерода и породили нужное им возбужденное состояние Ne 20(обозначаемое Ne 20*) в реакции

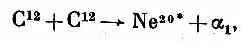
где a 1— это a-частица, или Не 4. Кое-какие из создаваемых таким образом возбужденных состояний Ne 20неустойчивы и распадаются таким путем:

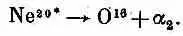
Значит, на опыте видны возникающие в реакции две a-частицы. Обозначим их a 1 и a 2; поскольку они вылетают с разными энер­гиями, их можно отличить друг от друга. Кроме того, выбирая a 1, имеющие нужную энергию, мы можем отобрать любые воз­бужденные состояния Ne 20.

Опыт ставился так, как показано на фиг. 16.9.

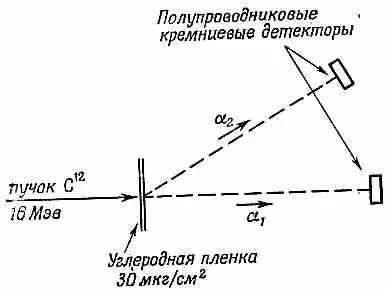
Фиг. 16.9. Размещение приборов в опыте по определению спина воз­бужденных состояний Ne 20.

Пучок ионов углерода с энергией 16 Мэв был направлен на углеродную пленку. Первая a-частица регистрировалась кремниевым детектором, настроенным на прием a-частиц с нужной энергией, движущихся вперед (по отношению к падающему пучку ионов С 12). Вторая a-частица регистрировалась счетчиком a 2, поставленным под углом q к a 1. Скорость счета сигналов совпа­дений от a 1и a 2измерялась как функция угла q.

Идея опыта в следующем. Прежде всего нужно знать, что спины С 12, О 16и a-частицы все равны нулю. Назовем направ­ление движения начальных частиц С 12направлением +z; тогда известно, что Ne 20*должен обладать нулевым моментом коли­чества движения относительно оси z . Ведь ни у одной из осталь­ных частиц нет спина; кроме того, С 12прилетает вдоль оси z и a 1улетает вдоль оси z, так что у них не может быть момента относительно этой оси. И каким бы ни был спин j ядра Ne 20*, мы знаем, что это ядро находится в состоянии | j , 0> . Что же случится, когда Ne 20*распадется на О 16и другую a-частицу? Что ж, a-частицу поймает счетчик a 2, а О 1 6, чтобы сохранить начальный импульс, вынужден будет уйти в противоположную сторону. Относительно новой оси (оси a 2) не может быть тоже никакой компоненты момента количества движения. А раз конечное состояние имеет относительно новой оси нулевой мо­мент количества движения, то у распада Ne 20*должна быть некоторая амплитуда того, что m ' =0, где m '— квантовое число компоненты момента количества движения относительно новой оси. Вероятность наблюдать a 2под углом q будет на самом деле равна квадрату амплитуды (или матричного эле­мента)