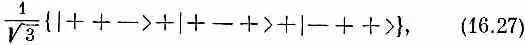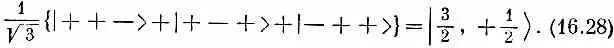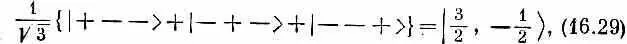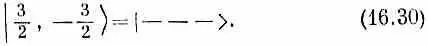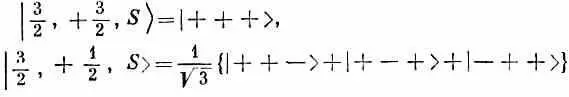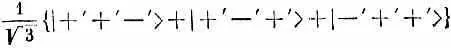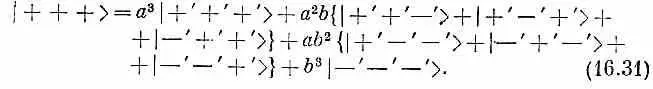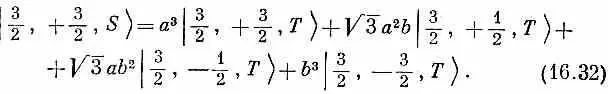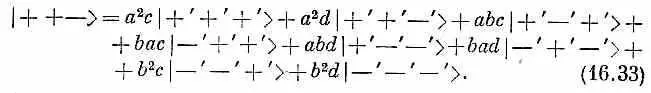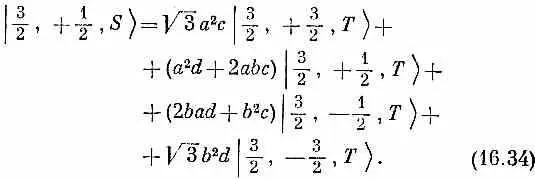Feynmann - Feynmann 9

|++->, |+-+>, |-++>, |+-->, |-+->,

|--+> или |---> . Ясно, однако, что их можно раз­бить на четыре группы, чтобы каждая соответствовала своему значению m . Прежде всего мы имеем |+++>, для которого m = 3/ 2. Затем имеется тройка состояний |++->, |+-+> и |-++> — каждое с двумя плюсами и одним минусом. Поскольку каждый из объектов со спином 1/ 2имеет равные шансы стать после поворота минусом, то каждая из этих трех комбинаций должна войти на равных паях. Поэто­му возьмем комбинацию

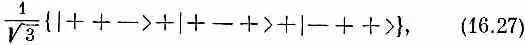
где множитель 1/Ц3 поставлен для нормировки. Если мы по­вернем это состояние вокруг оси z , то получим множитель e i j /2 для каждого плюса и e - i f /2 для каждого минуса. Каждое слагаемое в (16.27) умножится на e i j /2 , и общий множитель е i j / 2 мы вынесем за скобки. Такое состояние соответствует нашему представлению о состоянии с m = + 1/ 2; мы приходим к выводу, что

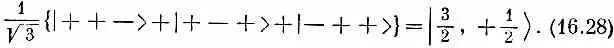
Точно так же можно написать

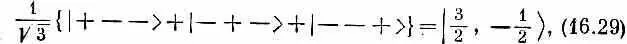
что соответствует состоянию с m = - 1/ 2. Заметьте, что мы берем только симметричные сочетания, у нас нет комбинаций, куда входят слагаемые со знаком минус. Они отвечали бы со­стояниям с таким же т, но с иным j . Это аналогично случаю спина 1, где (1/Ц2){|+->+|-+>} было состоянием | 1,0>, а (1/Ц2){|+->-|-+>} было состоянием | 0,0>. Наконец, мы имеем

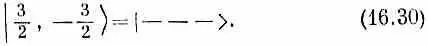
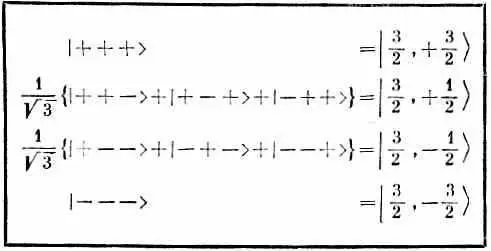
Эта четверка состояний сведена в табл. 16.1.

Таблица 16.1 · СВОДКА СОСТОЯНИЙ

Все, что нам теперь нужно сделать, это взять каждое состоя­ние, повернуть его вокруг оси у и посмотреть, сколько новых состояний оно создаст — пользуясь известной нам матрицей поворота для частицы спина 1/ 2. Можно поступать так же, как мы это делали в случае спина 1 [см. гл. 10, § 6 (вып. 8)]. (Только алгебры будет побольше.) Мы будем строго следовать идеям гл. 10 (вып. 8), так что подробных объяснений давать не будем. Состояния в системе S будут обозначаться

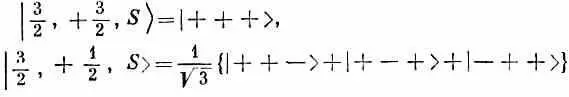
и т. д.; T -системой будет считаться система, повернутая вокруг оси у системы S на угол q. Состояния в T -системе будут обозна­чаться | 3/ 2, + 3/ 2, Т > , | 3/ 2, + 1/ 2, Т > и т. д. Ясно, что | 3/ 2, + 3/ 2, Т > это то же самое, что | +' + ' + ' > (штрихи всегда относятся к T -системе). Точно так же | 3/ 2, + 1/ 2, Т > будет равняться

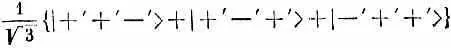
и т. д. Каждое |+'>-состояние в T -системе получается как из |+>-, так и из |->-состояний в системе S с помощью матрич­ных элементов из табл. 10.4 (вып. 8, стр. 267).

Если мы имеем тройку частиц со спином 1/ 2, то (10.47) надо заменить на

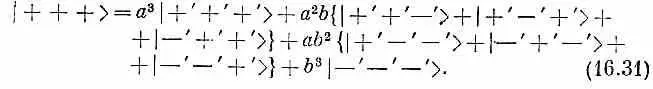
Пользуясь обозначениями табл. 10.4, получим вместо (10.48) уравнение

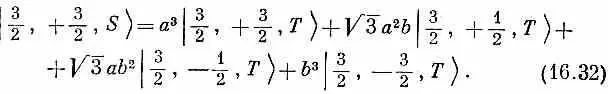
Это уже дает нам некоторые из наших матричных элементов < jT | iS > . Чтобы получить выражение для 3/ 2, + 1/ 2, S > мы дол­жны исходить из преобразования состояния с двумя плюсами и одним минусом. К примеру,

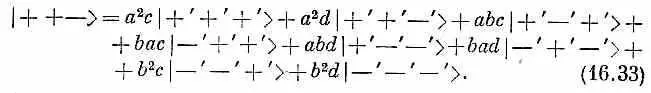
Добавляя два сходных выражения для + — +> и | — + +> и деля на ]/3, найдем

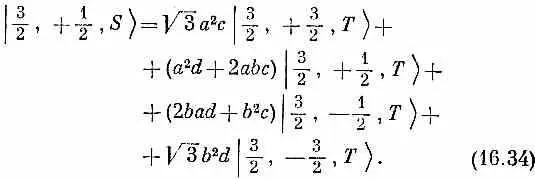
Продолжая этот процесс, мы найдем все элементы < j Т | iS > матрицы преобразования. Они приведены в табл. 16.2. Первый столбец получается из (16.32), второй — из (16.34). Последние два столбца были вычислены таким же способом. Теперь допустим, что T -система была повернута относительно S -системы на угол q вокруг ее оси у. Тогда а, b , с и d равны [см. (10.54), вып. 8]: а= d = cosq/2, с =- b =sinq/2. Под­ставляя это в табл. 16.2, получаем формулы, похожие на вторую половину табл. 15.2, но на этот раз для системы со спином 3/ 2.