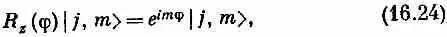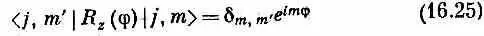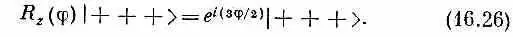Feynmann - Feynmann 9

Как мы видели раньше, любая система со спином, или «пол­ным моментом количества движения», j может существовать в одном из 2/ + 1 состояний, в которых z-компонента момента количества движения принимает одно из дискретных значе­ний j , j -1, j - 2, . . ., -( j -1), - j (все в единицах h ). Обозначая z-компоненту момента количества движения про­извольного выбранного состояния через mh , можно определить состояние момента количества движения, задав численные значения двух «квантовых чисел момента количества движения» j и m . Такое состояние можно отметить, указав вектор состоя­ния | j, m > . В случае частиц со спином 1/ 2могут быть два состоя­ния | 1/ 2, 1/ 2) и | 1/ 2, - 1/ 2> a состояния системы со спином 1 в этих обозначениях можно записать как |1, +1>, |1, 0>, | 1, -1> . У частицы со спином 0 может быть, конечно, лишь одно

состояние | 0, 0>.

Теперь мы можем посмотреть, что происходит, когда мы прое­цируем общее состояние | j , m > на представление, относящееся к повернутой системе осей. Прежде всего известно, что j — это число, которое характеризует систему, поэтому оно не меняется. При повороте осей мы получим просто смесь различных значе­ний т для одного и того же j . В общем случае появится амплиту­да того, что система в повернутой системе координат окажется в состоянии | j , m ' > , где m ' — новая z-компонента момента ко­личества движения. Значит, нам нужны матричные элементы < j , m ' | R | j , m > всевозможных поворотов. Мы уже знаем, что бывает, если поворот делается на угол j вокруг оси z . Новое состояние — это попросту старое, умноженное на e im j , у него по-прежнему то же значение т. Это можно записать так:

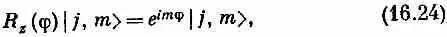
или, если вам больше нравится,

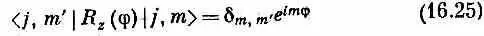
(где d m , m 'равно единице при m ' = m , и нулю в прочих случаях).

При поворотах вокруг любой другой оси возникает переме­шивание различных m -состояний. Можно было бы, конечно, попытаться подсчитать матричные элементы для произвольных поворотов, описываемых углами Эйлера b,a и g . Но будет легче, если мы вспомним, что самый общий такой поворот может быть составлен из трех поворотов R z (g), R y (a), R z (b); так что если мы знаем матричные элементы для поворотов вокруг оси y , то уже располагаем всем необходимым.

Как же нам найти матрицу поворота для поворота частицы со спином j на угол q вокруг оси у? Опираясь на основные за­коны (и на то, что уже было), это сделать нелегко. Мы так посту­пали со спином 1/ 2: вывели все, что нужно, пользуясь довольно сложными соображениями симметрии. Для спина 1 мы это про­делали уже иначе: рассмотрели частный случай, когда система со спином 1 складывается из двух систем со спином 1/ 2. Если вы последуете за нами и признаете правильным тот факт, что в общем случае ответы зависят только от спина j , а не от того, как скреплены между собой разные части системы со спином j , то мы сможем обобщить рассуждения для спина 1 на произвольный спин. Мы сможем, например, соорудить искусственную систему со спином 3/ 2из трех объектов со спином 1/ 2. Мы сможем даже избежать всяких усложнений, вообразив, что все они суть различные частицы — скажем, протон, электрон и мюон. Преобразуя каждый объект со спином 1/ 2, мы увидим, что происходит со всей системой — надо только вспомнить, что для комбинированного состояния все амплитуды перемножаются. Давайте посмотрим, как все это проходит.

Допустим, мы расположили все три объекта со спином 1/ 2спинами вверх; обозначим такое состояние |+++>. Если мы взглянем на него из системы координат, повернутой относительно оси z на угол j, то каждый плюс останется плюсом, но умно­жится на е i j /2 . Таких множителей у нас тройка, так что

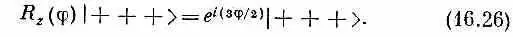
Ясно, что состояние |+++> — это как раз то, что мы назы­ваем состоянием m =+ 3/ 2, или состоянием | 3/ 2, + 3/ 2>.

Если мы затем повернем эту систему вокруг оси у, то у каж­дого из объектов со спином 1/ 2появится некоторая амплиту­да стать плюсом или стать минусом, так что вся система станет теперь смесью восьми возможных комбинаций |+++>,