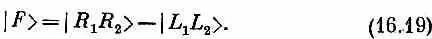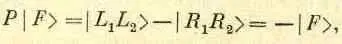Feynmann - Feynmann 9

А теперь мы покажем, что двухфотонная аннигиляция из состояния со спином 1 вообще невозможна. Могло бы показать­ся, что это не так, что если взять состояние с j =1, m =0, у которого момент количества движения относительно оси z равен нулю, то оно будет походить на состояние со спином 0 и поэтому распадется на два правых фотона. Конечно, изображен­ный на фиг. 16.7, а распад сохраняет момент количества движе­ния относительно оси z .

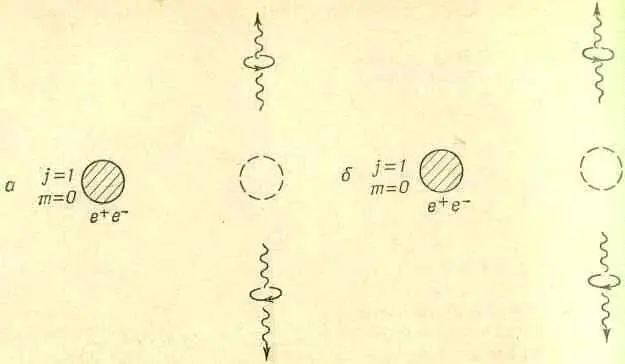
Фиг. 16.7. Для состояния позитрония с j = 1 процесс (а) и процесс (б), получаемый поворотом (а) вокруг оси у на 180°, в точности совпадают.

Но посмотрим, что будет, если мы повернем эту систему вокруг оси у на 180°; получится то, что показано на фиг. 16.7, б, т. е. конфигурация, в точности сов­падающая с фиг. 16.7, а. Обменялись местами два фотона и больше ничего. А ведь фотоны — это бозе-частицы; перестановка их местами не меняет знака амплитуды, так что амплитуда распада на конфигурацию, показанную на фиг. 16.7, б, должна быть такой же, как и на конфигурацию фиг, 16.7, а. Но мы предполо­жили, что у начального объекта спин был равен единице. А когда мы поворачиваем объект со спином 1 в состоянии с m =0 на 180° вокруг оси у, то его амплитуда меняет знак (см. табл. 15.2 для q=p, стр. 129). Значит, амплитуды обеих конфигура­ций на фиг. 16.7 должны иметь обратные знаки; частица со спи­ном 1 не может распадаться на два фотона.

Когда образуется позитроний, то можно ожидать, что в те­чение 1/ 4времени он будет превращаться в состояние со спином 0 и в течение 3/ 4времени — в состояние со спином 1 (с m = - 1,0 или +1). Так что 1/ 4времени будет происходить двухфотонная аннигиляция. Остальные 3/ 4времени двухфотонная аннигиляция происходить не может. Аннигиляция про­исходит, но на три фотона. Такой аннигиляции труднее дож­даться, и время жизни получается в 1000 раз дольше — около 10 -7 сек. Это и наблюдается на опыте. Аннигиляцией состояния со спином 1 мы подробнее заниматься не будем.

До сих пор мы, опираясь на сохранение момента количества движения, считали, что состояние позитрония с нулевым спином может превращаться в два правых фотона. Имеется и другая возможность: это состояние может превратиться в пару левы фотонов, как показано на фиг. 16.8. Следующий вопрос — како-

во соотношение между амплитудами этих двух типов распада? Это можно узнать, учтя сохранение четности.

Но для этого нам нужно знать четность позитрония. Физи­ки-теоретики показали (сложным путем, который нелегко пояс­нить), что четности электрона и позитрона (его античастицы) должны быть противоположны, так что основное состояние позитрония со спином 0 должно обладать отрицательной чет­ностью. Мы просто предположим, что четность отрицательна, и, поскольку мы получим согласие с экспериментом, мы сочтем это достаточно убедительным доводом.

Посмотрим же, что произойдет, если мы проделаем инверсию процесса на фиг. 16.6. При инверсии оба фотона меняют свои направления и поляризации. Обращенная картина выглядит так, как показано на фиг. 16.8.

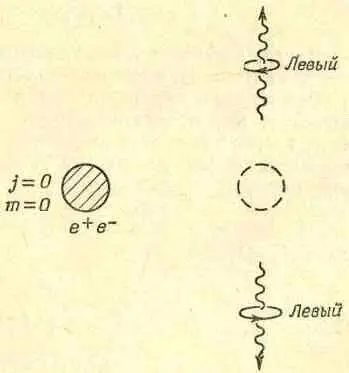
Фиг. 16.8 Другой мыслимый процесс аннигиляции позитрония.

Если считать, что четность по­зитрония отрицательна, то амплитуды процессов на фиг. 16.6 и 16.8 должны иметь обратные знаки. Пусть | R 1 R 2> — конеч­ное состояние на фиг. 16.6, где оба фотона правые, а | L 1 L 2 > — конечное состояние на фиг. 16.8, где оба фотона — левые. Ис­тинное конечное состояние (обозначим его | F >) должно быть таким:

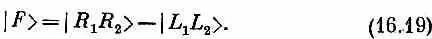
Тогда инверсия поменяет местами все R со всеми L и приведет к состоянию

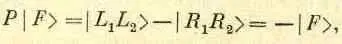
имеющему по сравнению с (16.19) знак минус. Значит, конечное состояние | F > обладает отрицательной четностью, совпадаю­щей с четностью первоначального состояния позитрония со спином 0. Это единственное конечное состояние, кото­рое сохраняет и момент количества движения и четность. Можно, конечно, вычислить амплитуду то­го, что произойдет распад в это состояние, но мы не будем этим заниматься, нас сейчас интересует только поляризация.