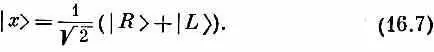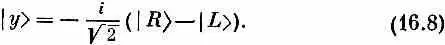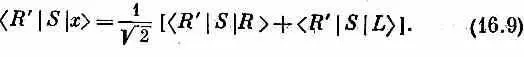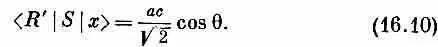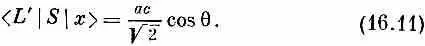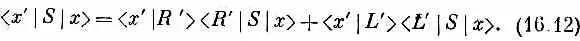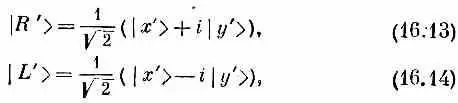Feynmann - Feynmann 9

Все это прекрасно, но допустим, что мы хотели бы начать с линейно поляризованного света. Чего можно было бы тогда ожидать? Если свет поляризован вдоль оси х, его можно пред­ставить как суперпозицию право- и левополяризованного по кругу света. Мы пишем [см. гл. 9, § 4 (вып. 8)]

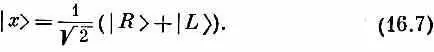
Или если свет поляризован вдоль оси у, то

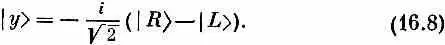
Ч то вы теперь хотите знать? Хотите знать амплитуду того, что х- поляризованный фотон рассеется под углом в как правый фотон? Пожалуйста. Примените для этого обычное правило комбинирования амплитуд. Сначала умножьте (16.7) на < R '| S . Вы получите

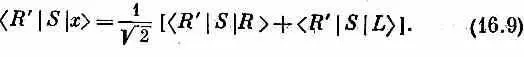
Теперь подставьте сюда (16.3) и (16.5). Получается

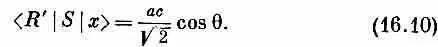
Если бы вам нужна была амплитуда того, что x-фотон рассеется как левый фотон, то вы бы получили

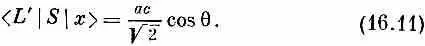
Наконец, представим, что вас заинтересовала амплитуда того, что x -поляризованный фотон рассеется, сохранив свою x -поляризацию. Значит, вам нужно знать <���х'| S | х > . Это мож­но записать так:

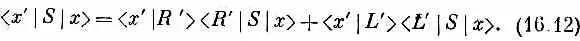
Если вы затем вспомните соотношения

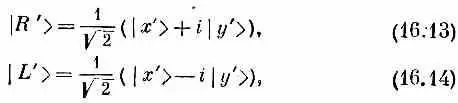
то из них последует

В итоге вы получите

Ответ, стало быть, состоит в том, что пучок x -поляризованного света рассеивается в направлении q (в плоскости xz ) с интен­сивностью, пропорциональной cos 2q. Если же нас интересует y -поляризованный свет, то

Иначе говоря, рассеянный свет полностью поляризован в x -направлении.

Здесь отметим интересную вещь. Формулы (16.17) и (16.18) точно соответствуют классической теории рассеяния света, которую мы излагали в гл. 32, § 5 (вып. 3), считая, что электрон связан с атомом линейной возвращающей силой, что действует он как классический осциллятор. Вы можете подумать: «А в классической теории все было куда проще; если она дает верный ответ, зачем забивать себе голову квантовой теорией?» Во-пер­вых, мы пока рассмотрели только один частный (хотя и частый) случай атома с возбужденным состоянием j =1 и с основным состоянием j =0. Если бы возбужденное состояние имело спин, равный 2, вы бы получили уже иные результаты. Во-вторых, нет причины, почему бы модель электрона, привязанного к пружинке и приводимого в движение колеблющимся электриче­ским полем, должна была бы быть верна для одиночного фотона. Правда, мы обнаружили, что она все же верна и что интен­сивность и поляризация оказываются какими надо. Так что в каком-то смысле мы в течение нашего курса лавировали где-то неподалеку от истины. В начале курса мы излагали теорию показателя преломления и рассеяния света, опираясь на клас­сические представления. А теперь мы показали, что квантовая теория в самых обычных случаях приводит к тому же результату. Мы фактически только что объяснили такое, скажем, явление, как поляризация дневного света, с помощью квантовомеханических рассуждений, а это единственный по-настоящему закон­ный путь.

Вообще все имеющие сегодня хождение классические теории должны быть в конечном счете подтверждены единственно пра­вильными квантовыми аргументами. Естественно, что все те вещи, на объяснения которых мы потратили прежде столько времени, были отобраны как раз из тех частей классической физики, которые еще подтверждаются квантовой механикой. Заметьте, что мы не обсуждали во всех деталях такие модели атома, в которых электроны двигались вокруг ядра по орбитам. Это потому, что такая модель не дает результатов, согласуемых с квантовой механикой. Но электрон на пружинке (хоть эта картина ничуть не смахивает на настоящий атом) действительно с ней согласуется, и потому мы применяли эту модель в теории показателя преломления.