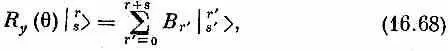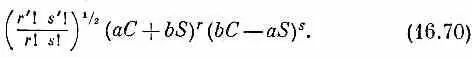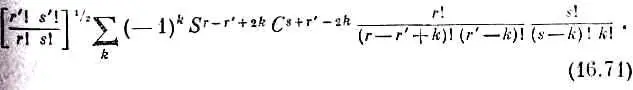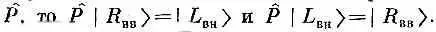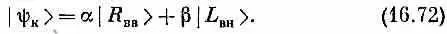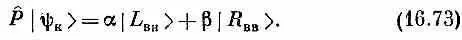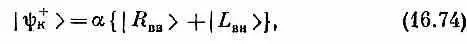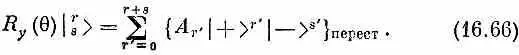
Теперь разделим каждое А r ' на множитель [ ( r '+ s ')\ l r ' ! s ' !] l /2 и обозначим частное через В r . Тогда (16.66) превратится в
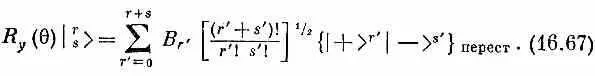
[Можно просто сказать, что требование, чтобы (16.67) совпадало с (16.65), определяет B r ’]
Если так определить В r ' , то оставшиеся множители в правой части (16.67) будут как раз состояниями 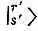 . Итак, имеем
. Итак, имеем
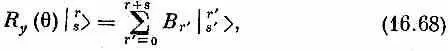
где s' всегда равняется r + s - r '. А это, конечно, означает, что коэффициенты В r ' и есть искомые матричные элементы

Теперь, чтобы найти B r ', остается немного: лишь пробиться через алгебру.
Сравнивая (16.67) с (16.65) и вспоминая, что r '+ s '= r + s , мы видим, что B r '— это просто коэффициент при a r ' b s ' в выражении
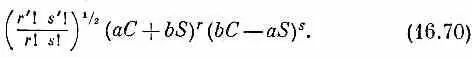
Осталась лишь нудная работа разложить скобки по биному Ньютона и собрать члены с данными степенями а и b . Если вы все это проделаете, то увидите, что коэффициент при а r ' b s ' в (16.70) имеет вид
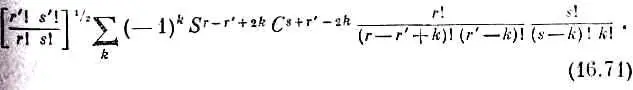
Сумма берется по всем целым k , при которых аргументы факториалов больше или в крайнем случае равны нулю. Это выражение и есть искомый матричный элемент.
В конце надо вернуться к нашим первоначальным обозначениям j , m и m ', пользуясь формулами
r=j+-m, r '= j + m' , s=j-m , s'=j-m' . Проделав эти подстановки, получим уравнение (16.34) из § 4.
Добавление 2. Сохранение четности при испускании фотона
В § 1 мы рассмотрели испускание света атомом, который переходит из возбужденного состояния со спином 1 в основное состояние со спином 0. Если спин возбужденного состояния направлен вверх ( m =+1), то атом может излучить вверх вдоль оси + z правый фотон или вдоль оси -z левый. Обозначим эти два состояния фотона | R вв> и | L вн>. Ни одно из них не обладает определенной четностью. Если оператор четности обозначить
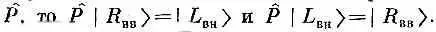
Что же тогда будет с нашим прежним доказательством, что атом в состоянии с определенной энергией должен иметь определенную четность, и с нашим утверждением, что четность в атомных процессах сохраняется? Разве не должно конечное состояние в этой задаче (состояние после излучения фотона) иметь определенную четность? Да, должно, если только мы рассмотрим полное конечное состояние, в которое входят амплитуды излучения фотонов под всевозможными углами. А в § 1 мы рассматривали только часть полного конечного состояния.
Если вы хотите, можно рассмотреть только конечные состояния, у которых действительно определенная четность. Например, рассмотрим конечное состояние |y k>, у которого есть некоторая амплитуда а оказаться правым фотоном, движущимся вдоль оси +z, и некоторая амплитуда b оказаться левым фотоном, движущимся вдоль оси -z. Можно написать
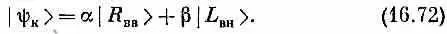
Оператор четности, действуя на это состояние, дает
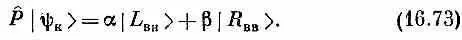
Это состояние совпадает с ± |y к> либо при b=a, либо при b=-a. Так что конечное состояние с положительной четностью таково:
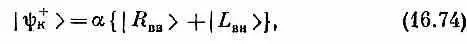
Читать дальше

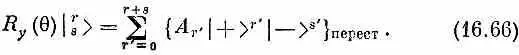
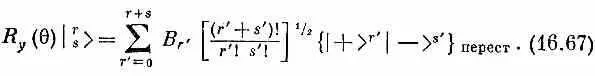
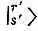 . Итак, имеем
. Итак, имеем