Feynmann - Feynmann 7

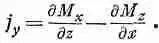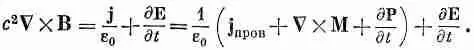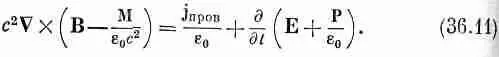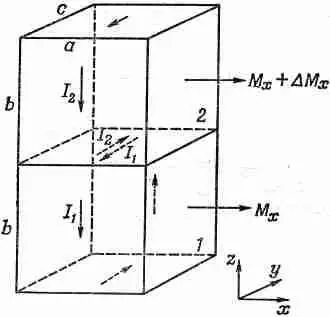
Фиг. 36.6. Два кубика, распо­ложенных один над другим, то­же могут давать вклад в j y .

Воспользовавшись только что проведенными рассуждениями, мы можем показать, что эта поверхность будет давать в величину j yвклад, равный dM x / dz . Только эти поверх­ности и будут давать вклад в y-компоненту тока, так что пол­ная плотность тока в направлении оси у получается равной

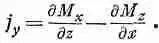
Определяя токи на остальных гранях куба или используя тот факт, что направление оси z было выбрано совершенно произ­вольно, мы можем прийти к заключению, что вектор плотности тока действительно определяется выражением .

j= СX M.

Итак, если вы решили описывать магнитное состояние ве­щества через средний магнитный момент единицы объема М, то оказывается, что циркулирующие атомные токи эквивалент­ны средней плотности тока в веществе, определяемой выраже­нием (36.7). Если же материал обладает вдобавок еще диэлект­рическими свойствами, то в нем может возникнуть и поляри­зационный ток j пол = d P / dt . А если материал к тому же и про­водник, то в нем может течь и ток проводимости j пров. Таким образом, полный ток можно записать как

J = J пр o в+ СXM+ д P / д t; (36.10)

§ 2. Поле Н

Теперь можно подставить выражение для тока (36.10) в уравнение Максвелла. Мы получаем

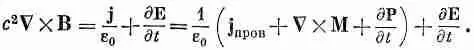
Слагаемое с Мможно перенести в левую часть: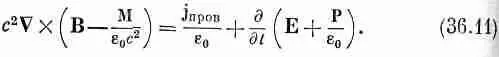

Как мы уже отмечали в гл. 32, иногда удобно записывать ( Е+ Р/e 0) как новое векторное поле D/e 0. Точно так же удобно ( В - М/e 0с 2) записывать в виде единого векторного поля. Такое поле мы обозначим через Н, т. е.

H= В- M/(e 0c 2). (36.12)

После этого уравнение (36.11) принимает вид

e 0c 2 СX H= j np ов+ д D/ д t. (36.13)

Выглядит оно просто, но вся его сложность теперь скрыта в буквах Dи Н.

Хочу предостеречь вас. Большинство людей, которые при­меняют систему СИ, пользуются другим определением Н. На­зывая свое поле через Н'(они, конечно, не пишут штриха), они определяют его как

Н'=e 0с 2 В- М. (36.14)

(Кроме того, величину e 0с 2они обычно записывают в виде l/m 0, так что появляется еще одна постоянная, за которой все время нужно следить!) При таком определении уравнение (36.13) будет выглядеть еще проще:

СX H' = j npo в+ д D/ д t. (36.15)

Но трудность здесь заключается в том, что такое определение, во-первых, не согласуется с определением, принятым теми, кто не пользуется системой СИ, и, во-вторых, поля Н'и Визме­ряются в различных единицах. Я думаю, что Нудобнее изме­рять в тех же единицах, что и В, а не в единицах М, как Н'. Но если вы собираетесь стать инженером и проектировать транс­форматоры, магниты и т. п., то будьте внимательны. Вы столк­нетесь со множеством книг, где в качестве определения Ниспользуется уравнение (36.14), а не (36.12), а в других книгах, особенно в справочниках о магнитных материалах, связь между Ви Нтакая же, как и у нас. Нужно быть внимательным и по­нимать, какое где использовано соглашение.

Одна из примет, указывающих нам на соглашение,— это единицы измерения. Напомним, что в системе СИ величина В, а следовательно, и наше Низмеряются в единицах вб/м 2 (1 вб/м 2 =10 000 гс). Магнитный же момент (т. е. произведение тока на площадь) в той же системе СИ измеряется в единицах а · м 2 . Тогда намагниченность Мимеет размерность а / м. Размерность Н'та же, что и размерность М. Нетрудно видеть, что это согла­суется с уравнением (36.15), поскольку у имеет размерность обратной длины.