Feynmann - Feynmann 7

Хотя производная dM z / dy в точке С равна нулю, производная dM z / dx будет большой и положительной. Выражение (36.7) говорит, что в отрицательном направлении оси у течет ток огромной плотности. Это согласуется с нашим представлением о поверхностном токе, текущем вокруг цилиндра.

Теперь мы можем найти плотность тока в более сложном случае, когда намагниченность в материале меняется от точки к точке. Качественно нетрудно понять, что если в двух сосед­них областях намагниченность различная, то полной компен­сации циркулирующих токов не происходит, поэтому полный ток внутри материала не равен нулю. Именно этот эффект мы и хотим получить количественно.

Прежде всего вспомните, что в гл. 14, § 5 (вып. 5), мы вы­яснили, что циркулирующий ток I создает магнитный момент

m = I А, (36.9)

где А— площадь, ограниченная контуром тока (фиг. 36.3).

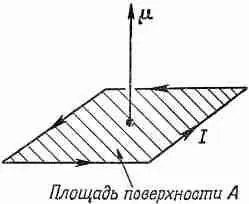
Фиг. 36.3 . Дипольный момент m кон тура тока равен IA .

Рассмотрим маленький прямо­угольный кубик внутри намаг­ниченного материала (фиг. 36.4).

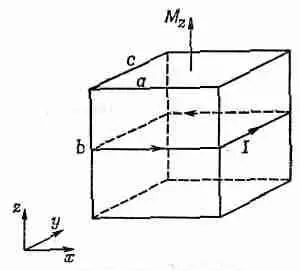
Фиг. 36.4. Небольшой намагничен­ный кубик эквивалентен циркули­рующему поверхностному току.

Пусть кубик будет так мал, что намагниченность внутри него можно считать однородной. Если компонента намагниченности этого кубика в направлении оси z равна М z , то полный эффект будет таким, как будто по вертикальным граням течет поверх­ностный ток. Величину этого тока мы можем найти из ра­венства (36.9). Полный магнитный момент кубика равен про­изведению намагниченности на объем:

m = M z ( abc ),

откуда, вспоминая, что площадь равна ас, получаем

I =М z b .

Другими словами, на каждой из вертикальных поверхностей величина тока на единицу длины по вертикали равна М z .

Представьте теперь два таких маленьких кубика, располо­женных рядом друг с другом (фиг. 36.5).

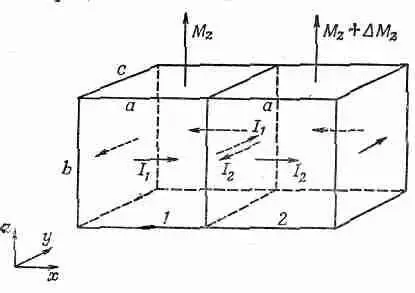
Фиг. 36.5. Если на­магниченность двух соседних кубиков раз­лична, то на их гра­нице течет поверх­ностный ток.

Кубик 2 несколько смещен по отношению к кубику 1, поэтому его вертикальная компонента намагниченности будет немного другой, скажем M z+DМ z. Теперь полный ток на поверхности между этими двумя кубиками будет слагаться из двух частей. По кубику 1 в положительном направлении по оси у течет ток I 1, а по кубику 2 в отрицательном направлении течет ток I 2. Полный поверхностный ток в положительном направлении оси у будет равен сумме

I=I 1-I 2= М z b-( М z + D М z) b =-DM zb.

Величину D М г можно записать в виде произведения произ­водной от M z по х на смещение кубика 2 относительно кубика 1, которое как раз равно а:

DM z=( д M z/ д x)а. Тогда ток, текущий между двумя кубиками, будет равен

I=(- д M z/ д x)ab.

Чтобы связать ток I со средней объемной плотностью тока j, необходимо понять, что этот ток на самом деле размазан по некоторой области поперечного сечения. Если мы вообразим, что такими маленькими кубиками заполнен весь объем мате­риала, то за такое сечение (перпендикулярное оси х) может быть выбрана боковая грань одного из кубиков. Теперь вы видите, что площадь, связанная с током, как раз равна площади ab одной из фронтальных граней. В результате получаем

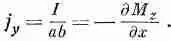
Наконец-то у нас начинает получаться ротор М.

Но в выражении для j y должно быть еще одно слагаемое, связанное с изменением x-компоненты намагниченности с изме­нением z. Этот вклад в jпроисходит от поверхности между двумя маленькими кубиками, поставленными друг на друга (фиг. 36.6).