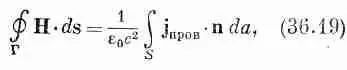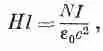Feynmann - Feynmann 7

Те, кто работает с электромагнитами, привыкли измерять поле Н(определенное как Н') в ампер-витках/метр, имея при этом в виду витки провода в обмотке. Но «виток» ведь фактически величина безразмерная, и она не должна вас смущать. Посколь­ку наше Н равно H '/ e 0 c 2 , то, если вы пользуетесь системой СИ, Н (в вб/м) равно произведению 4p·10 -7на Н'(в а/м). Может быть, более удобно помнить, что Н (в гс) равно 0,0126 H ' (в а/м).

Здесь есть еще одна ужасная вещь. Многие люди, исполь­зующие наше определение Н, решили назвать единицы измере­ния Ни В по-разному ! И даже несмотря на одинаковую размер­ность, они называют единицу В гауссом, а единицу Н— эрсте­дом (конечно, в честь Гаусса и Эрстеда). Таким образом, во многих книгах вы найдете графики зависимости В в гауссах от Нв эрстедах. На самом деле это одна и та же единица, равная 10 -4единиц СИ. Эту неразбериху в магнитных единицах мы увековечили в табл. 36.1.

Таблица 36.1 · ЕДИНИЦЫ МАГНИТНЫХ ВЕЛИЧИН

§ 3. Кривая намагничивания

Рассмотрим теперь некоторые простые случаи, когда маг­нитное поле остается постоянным или изменения поля настолько медленны, что можно пренебречь d D / dt по сравнению с j npo в. В этом случае поля подчиняются уравнениям

СX B=0, (36.16)

СX H=j пров/e 0c 2, (36.17)

H= B- M/e 0c 2. (36.18)

Предположим, что у нас есть железный тор с намотанной на него медной проволокой, как это показано на фиг. 36.7, а.

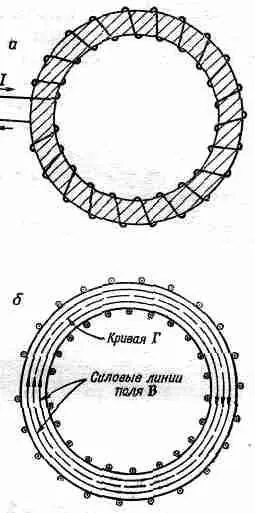
Фиг. 36.7. Железный тор, обмотанный витками изолированного провода (а), и его поперечное сечение (б). Показаны силовые линии.

Пусть по проводу течет ток I. Каково при этом магнитное поле? Оно будет сосредоточено главным образом внутри железа, причем там (см. фиг. 36.7, б) силовые линии должны быть круговыми. Вследствие постоянства потока В его дивергенция равна нулю, и уравнение (36.16) удовлетворяется автоматически. Запишем затем уравнение (36.17) в другой форме, проинтегрировав его по замкнутому контуру Г, показанному на фиг. 36.7, б. Из теоремы Стокса мы получаем

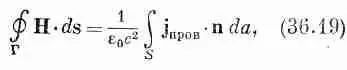
где интеграл от jберется по поверхности S , ограниченной кон­туром Г. Каждый виток обмотки пересекает эту поверхность один раз, поэтому каждый виток дает в интеграл вклад, равный I , а пос­кольку всего витков N штук, то интеграл будет равен N I . Из симметрии нашей задачи видно, что В одинаково на всем контуре Г, если, конечно, намагниченность, а следовательно, и поле Нтоже постоянны на контуре Г. Уравнение (36.19) при таких условиях принимает вид

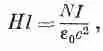
где l —длина кривой Г. Таким образом,

Именно из-за того что в задачах подобного типа поле Нпрямо пропорционально намагничивающему току, оно иногда назы­вается намагничивающим.

Единственное, что нам теперь требуется,— это уравнение, связывающее Нс В. Однако такого уравнения просто не суще­ствует! У нас есть, конечно, уравнение (36.18), но от него мало проку, ибо в ферромагнитных материалах типа железа оно не дает прямой связи между Ми В. Намагниченность М зависит от всей предыдущей истории данного образца железа, а не толь­ко от того, каково поле В в данный момент и как оно изменялось раньше.

Впрочем, еще не все потеряно. В некоторых простых слу­чаях мы все же можем найти решение. Если взять ненамагни­ченное железо, скажем, отожженное при высокой температуре, то для такого простого тела, как тор, магнитная предыстория всего железа будет одной и той же. Затем из экспериментальных измерений мы можем кое-что сказать относительно М, а следо­вательно, и о связи между Ви Н. Из уравнения (36.20) видно, что поле Ввнутри тора равно произведению некоторой посто­янной на величину тока в обмотке I. А поле Вможно измерить интегрированием по времени э.д.с. в намагничивающей обмотке, изображенной на рисунке (или в дополнительной обмотке, на­мотанной поверх нее). Эта э.д.с. равна скорости изменения по­тока В, так что интеграл от э.д.с. по времени равен произведе­нию Вна площадь поперечного сечения тора.