Feynmann - Feynmann 6a

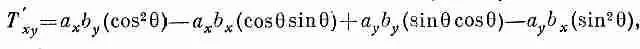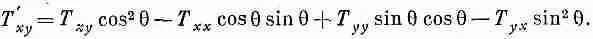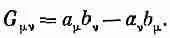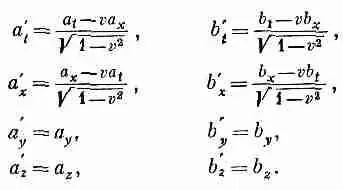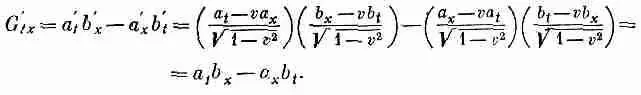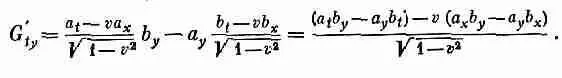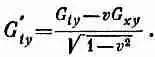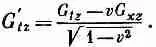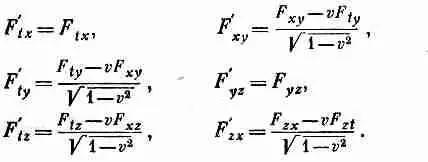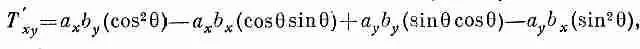
Аналогичные вещи происходят и с другими компонентами. Девять компонент изобретенной нами величины T ij., разу­меется, тоже изменяются. Например, T xy =а х b у переходит в

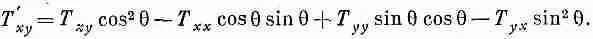
или

Каждая компонента T ij — это линейная комбинация ком­понент t ij .

Итак, мы обнаружили, что из векторов можно сделать не только векторное произведение aXb, три компоненты которого преобразуют подобно вектору. Искусственно мы из двух векто­ров t ij . можем сделать «произведение» другого сорта. Девять его компонент преобразуются при вращении по сложным правилам, которые можно выписать. Подобный объект, требующий для своего описания вместо одного индекса два, называется тензо­ром. Мы построили тензор «второго ранга», но так же можно поступить и с тремя векторами и получить тензор третьего ранга, а из четырех векторов — тензор четвертого ранга и т. д. Тензором первого ранга является вектор.

Суть всего этого разговора в том, что наше электромагнитное поле F m v — тоже тензор второго ранга, так как у него два индек­са. Однако это уже тензор в четырехмерном пространстве. Он преобразуется специальным образом, и через минуту мы найдем его. Это просто произведение векторных преобразований. Если у тензора F m vвы переставите индексы, то он изменит свой знак. Это особый вид тензора, и называется он антисимметричным. Иначе говоря, электрическое и магнитное поля являются частью антисимметричного тензора второго ранга в четырех­мерном пространстве.

Вот какой мы прошли длинный путь. Помните, мы начали с определения, что такое скорость? А теперь мы уже рассуждаем о «тензоре второго ранга в четырехмерном пространстве».

Теперь нам нужно найти закон преобразования F m v . Сделать это нетрудно — мороки только много,— шевелить мозгами особенно не нужно, а вот потрудиться все же придется. Един­ственное, что мы должны найти,— это преобразование Лоренца величины С m A v — С v A m . Так как С m — просто специальный слу­чай вектора, то мы будем работать с общей антисимметричной

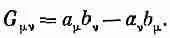
комбинацией векторов, которую можно назвать G m v :

(26.20)

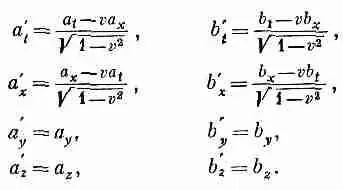
(Для наших целей а м следует, в конце концов, заменить на С m , а b m —на потенциал А m .) Компоненты а m и b m преобразуются по формулам Лоренца:

(26.21)

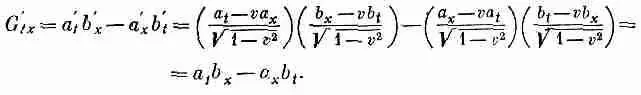
Теперь преобразуем компоненты G m v. Начнем с G tx :

Но ведь это просто G tx . Таким образом, мы получили простой

результат G’ tx = G tx .

Возьмем еще одну компоненту:

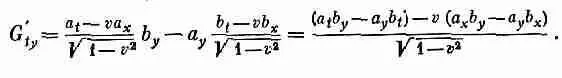
Итак, получается

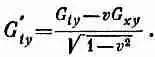
И, конечно, точно таким же образом

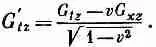
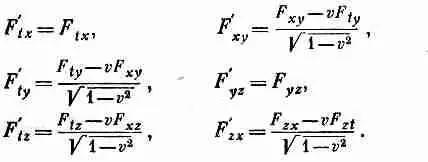
А теперь ясно, как ведут себя все остальные компоненты. Давайте составим таблицу преобразований всех шести членов; только теперь мы будем все писать для величин F m v :

(26.22)

Разумеется, по-прежнему у нас F m v =— f ' m v , a F ' mm =0.

Итак, мы имеем преобразования электрических и магнитных полей. Единственное, что нам нужно сделать,— это заглянуть в табл. 26.1 и узнать, что означает для векторов Е и В преобра­зование, записанное для F м v . Речь идет о простой подстановке. Чтобы можно было видеть, как это все выглядит в обычных сим­волах, перепишем наши преобразования компонент поля в виде табл. 26.2.