Глав а 22
ЦЕПИ ПЕРЕМЕННОГО ТОКА
§ 1. Импедансы
§ 2. Генераторы
§ 3. Сети идеальных элементов; правила Кирхгофа
S 4. Эквивалентные контуры
§ 5. Энергия
§ 6. Лестничная сеть
§ 7. Фильтры
§ 8. Другие элементы цепи
Повторить : гл.2 (вып. 2) «Алгебра»; гл. 23 (вып. 2) «Резонанс»;
гл. 25 (вып. 2) «Линейные системы и обзор»
§ 1. Импедансы
В основном наши усилия при чтении этих лекций были направлены на то, чтобы получить полные уравнения Максвелла. В предыдущих двух главах мы обсудили следствия этих уравнений. Выяснилось, что они содержат объяснение всех статических явлений, которые мы изучали раньше, и явлений электромагнитных волн и света — вопроса, подробно изучавшегося в самом начале нашего курса. Уравнения Максвелла дают и то и другое, смотря по тому, где эти поля вычисляются: поблизости от токов и зарядов или же вдали от них. Есть и промежуточная область, но о ней ничего интересного сказать нельзя; там никаких особых явлений не происходит.
Но в электромагнетизме остается еще несколько вопросов, которые стоит осветить. Надо будет обсудить вопрос связи относительности и уравнений Максвелла, т. е. выяснить, что произойдет, если на уравнения Максвелла посмотреть из движущейся системы координат. Важен еще и вопрос о сохранении энергии в электромагнитных системах. Кроме того, существует обширная область электромагнитных свойств материалов; до сих пор мы рассматривали только электромагнитные поля в пустом пространстве, если не считать изучения свойств диэлектриков. Да и при изучении света все еще оставалось несколько вопросов, которые хотелось бы рассмотреть еще раз с точки зрения уравнений поля.
В частности, надо бы еще раз вернуться к вопросу о показателе преломления (особенно у плотных веществ). Наконец, интересны явления, связанные с волнами, заключенными внутри ограниченной области пространства. Мы кратко коснулись этой проблемы, когда изучали звуковые волны. Но уравнения Максвелла тоже приводят к решениям, которые представляют волны электрических и магнитных полей, замкнутые в некотором объеме. В одной из последующих глав мы рассмотрим этот вопрос, имеющий важные технические применения. И чтобы подойти к нему, мы начнем с того, что изложим свойства электрических цепей при низких частотах. После этого мы сможем сравнить такие системы, когда к уравнениям Максвелла применимо почти статическое приближение, и системы, в которых преобладают высокочастотные эффекты.
Итак, снизойдем с величественных и труднодоступных высот последних нескольких глав и обратим свой взор на сравнительно низменную задачу — задачу об электрических цепях. Впрочем, мы убедимся в том, что даже столь мирские дела оказываются весьма запутанными, если в них вникнуть достаточно глубоко.
В гл. 23 и 25 (вып. 2) мы уже обсуждали некоторые свойства электрических цепей (контуров). Теперь мы повторим часть изложенного там материала, но более подробно. Мы по-прежнему будем иметь дело с линейными системами и с напряжениями и токами, которые меняются синусоидально; поэтому мы можем представить все напряжения и токи в виде комплексных чисел, пользуясь экспоненциальными обозначениями, введенными в гл. 22 (вып. 2). Так, меняющееся во времени напряжение V ( t ) будет записываться в виде

(22.1)
где  — комплексное число, не зависящее от t . При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V ( t ) представляется действительной частью комплексной функции в правой части уравнения.
— комплексное число, не зависящее от t . При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V ( t ) представляется действительной частью комплексной функции в правой части уравнения.

Подобным же образом и все другие меняющиеся во времени величины будут считаться изменяющимися синусоидально с той же частотой w. Мы будем писать
(22.2)
и т. д.
Большей частью мы будем писать уравнения, пользуясь обозначениями V, I, e , ...
(вместо 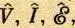 ...), помня при этом, что они изменяются со временем всегда так, как в (22.2).
...), помня при этом, что они изменяются со временем всегда так, как в (22.2).
В прежних наших рассуждениях об электрических цепях мы полагали, что такие вещи, как индуктивность, емкость и сопротивление, вам знакомы. Сейчас мы немного подробнее объясним, что понимают под этими идеализированными элементами схем. Начнем с индуктивности.
Читать дальше


 — комплексное число, не зависящее от t . При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V ( t ) представляется действительной частью комплексной функции в правой части уравнения.
— комплексное число, не зависящее от t . При этом, конечно, подразумевается, что настоящее переменное по времени напряжение V ( t ) представляется действительной частью комплексной функции в правой части уравнения.
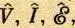 ...), помня при этом, что они изменяются со временем всегда так, как в (22.2).
...), помня при этом, что они изменяются со временем всегда так, как в (22.2).










