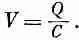Feynmann - Feynmann 6a

(22.5)

Для индуктивности мы имеем

(22.6)

Фиг. 22.2. Емкость (или конденсатор).

Рассмотрим с этой точки зрения емкость . Она состоит из двух проводящих пластин (обкладок), от которых к нужным за­жимам отходят два провода. Пластины могут быть любой формы и часто отделяются друг от друга каким-нибудь диэлектриком. Это схематически изображено на фиг. 22.2. Мы снова делаем несколько упрощающих предположений. Мы считаем, что пла­стины и провода — идеальные проводники, а изоляция между пластинами тоже идеальна, так что через нее никакие заряды с пластины на пластину перейти не могут. Затем мы предпола­гаем, что проводники находятся близко друг от друга, но зато аначительно удалены ото всех остальных проводников, так что все линии поля, выйдя из одной пластины, непременно окан­чиваются на другой. И тогда заряды на пластинах всегда равны и противоположны друг другу, причем по величине намного превосходят величину заряда на поверхности проводов. И на­конец, мы считаем, что поблизости от конденсатора магнитных полей нет.

Рассмотрим теперь контурный интеграл от Е вдоль замкну­той петли, которая начинается на клемме а, проходит внутри провода до верхней обкладки конденсатора, перескакивает про­межуток между пластинами, проходит с нижней обкладки на клемму b и возвращается к клемме а по пространству снаружи конденсатора. Раз магнитного поля нет, контурный интеграл от Е по этому замкнутому пути равен нулю. Интеграл можно раз­бить на три части:

Интеграл вдоль проводов равен нулю, потому что внутри идеаль­ных проводников электрического поля не бывает. Интеграл от зажима b до а снаружи конденсатора равен разности потенциалов между клеммами со знаком минус. А поскольку мы считаем, что обкладки как-то изолированы от прочего мира, то общий заряд двух обкладок должен быть равен нулю; и если на верх­ней обкладке есть заряд Q , то на нижней имеется заряд — Q . Раньше мы уже видели, что если заряды двух проводников рав­ны и противоположны, +Q и - Q , то разность потенциалов между ними есть Q / C , где С — емкость этих проводников. Из (22.7) следует, что разность потенциалов между зажимами а и b равна разности потенциалов между обкладками. Поэтому

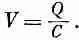
Электрический ток I, втекающий в конденсатор через клемму а (и покидающий его через клемму b ), равен dQ / dt — быстроте изменения электрического заряда на обкладках. Записывая dV / dt в виде iwV, можно связь между током и напряжением для конденсатора дать в следующем виде:

или

(22.8)

Тогда импеданс z конденсатора равен

(22.9)

Третий элемент, который нужно рассмотреть,— это сопро­тивление. Но, поскольку мы пока еще не рассматривали элек­трических свойств реальных веществ, мы не готовы обсуждать то, что творится внутри реального проводника. Придется просто принять как факт, что внутри реальных веществ могут суще­ствовать электрические ноля, что эти поля порождают поток электрического заряда (т. е. ток) и что этот ток пропорционален интегралу электрического поля от одного конца проводника до другого. Затем надо представить себе идеальное сопротивление, сделанное так, как показано на фиг. 22.3. Два провода, которые мы считаем идеальными проводниками, тянутся от клемм а и b к двум концам бруска, сделанного из материала, оказываю­щего сопротивление току. Следуя нашей обычной линии рас­суждений, приходим к выводу, что разность потенциалов между зажимами а и b равна контурному интегралу от внешнего элек­трического поля, равному также контурному интегралу от электрического поля по пути, проходящему через брусок.