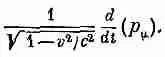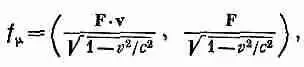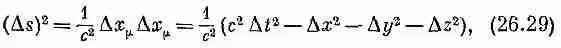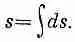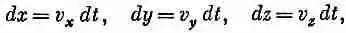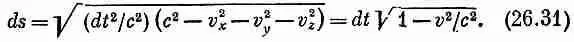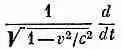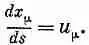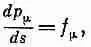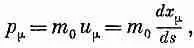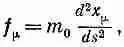Feynmann - Feynmann 6a

Итак, вторая гипотеза: четырехвектором должна быть ве­личина

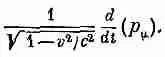
(26.27)

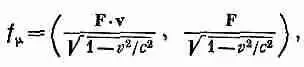
Но что такое v? Это уже скорость частицы, а не скорость системы координат! Таким образом, обобщением силы на четырехмерное пространство будет величина f m:

(26.28)

которую мы назовем «4-силой». Она уже четырехвектор, и ее пространственными компонентами будут уже не F, а

F/Ц(1-v 2/c 2).

Почему же f mчетырехвектор? Неплохо бы понять, что это за таинственный множитель 1/Ц(1-v 2/с 2). Так как мы встре­чаемся с ним уже второй раз, то самое время посмотреть, почему производная d / dt всегда должна входить с одним и тем же

множителем. Ответ заключается вот в чем. Когда мы берем производную по времени некоторой функции х, то подсчитываем приращение D х за малый интервал D t переменной t . Но в другой

системе отсчета интервал At может соответствовать изменению как t ', так и х', так что при изменении только t ' изменение х будет другим. Для наших дифференцирований следовало бы найти такую переменную, которая была бы мерой «интервала» в пространстве-времени и оставалась бы той же самой во всех системах отсчета. Когда в качестве этого интервала мы принимаем приращение D х, то оно будет тем же во всех системах отсчета. Когда частица «движется» в четырехмерном пространстве, то возникают приращения как D t , так и D х, D y , D z . Можно ли из них сделать интервал? Да, они образуют компоненты приращения четырехвектора х m =(с t , х, у, г), так что, если определить величину D s через

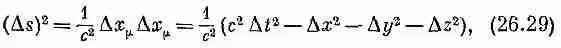
что представляет четырехмерное скалярное произведение, то в ней мы приобретаем настоящий скаляр и можем пользоваться им для измерения четырехмерного интервала. Исходя из вели­чины As или ее предела ds , мы можем определить параметр

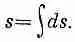
Хорошим четырехмерным оператором будет и производ­ная по s , т. е. d / ds , так как она инвариантна относительно пре­образований Лоренца.

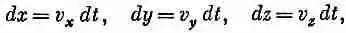
Для движущейся частицы ds легко связывается с dt . Для точечной частицы

(26.30)

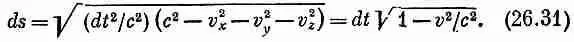
а

Таким образом, оператор

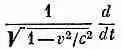
есть инвариантный оператор. Если подействовать им на любой четырехвектор, то мы получим другой четырехвектор. Например, если мы действуем им на ( ct , x , у, z ), то получаем четырехвектор скорости

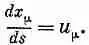
Теперь мы видим, почему Ц(l- v 2 / c 2 ) поправляет дело.

Инвариантная переменная s — очень полезная физическая величина. Ее называют «собственным временем» вдоль траекто­рии частицы, ибо в системе, в любой момент движущейся вместе с частицей, ds просто равно интервалу времени. (В этой системе Dx=Dy=Dz=0, a Ds=Dt.) Если вы представите себе часы, скорость хода которых не зависит от ускорения, то, двигаясь вместе с частицей, такие часы будут показывать время s.

Теперь можно вернуться назад и записать закон Ньютона (подправленный Эйнштейном) в изящной форме:

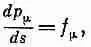
(26.32)

где f mопределяется формулой (26.28). Импульс же р m может быть записан в виде

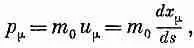
(26.33)

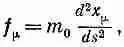
где координаты x m =( ct , х, у, z ) описывают теперь траекторию частицы. Наконец, четырехмерные обозначения приводят нас к очень простой форме уравнений движения:

(26.34)

напоминающей уравнения F=ma. Важно отметить, что урав­нения (26.34) и F=ma — вещи разные, ибо четырехвекторная форма уравнения (26.34) содержит в себе релятивистскую ме­ханику, которая при больших скоростях отличается от механики Ньютона. Это абсолютно непохоже на случай уравнений Максвелла, где нам нужно был о переписать уравнения в реляти­вистской форме, совершенно не изменяя их смысла, а изменяя лишь обозначения.