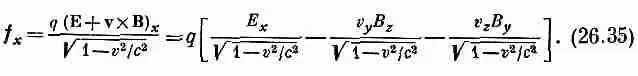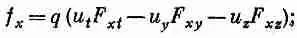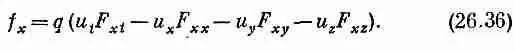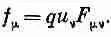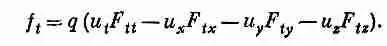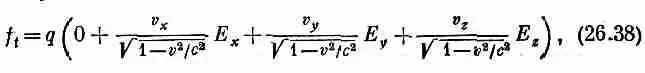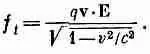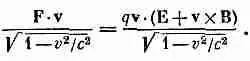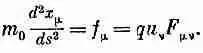Feynmann - Feynmann 6a

Вернемся теперь к уравнению (26.24) и посмотрим, как в четырехвекторных обозначениях записывается правая часть.

Три компоненты F, поделенные на Ц(1-v 2/c 2), составляют про­странственные компоненты f m, так что

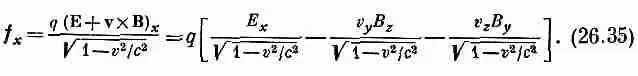
Теперь мы должны подставить все величины в их релятивистских обозначениях. Прежде всего c/Ц(1- v 2 / c 2 ), v y / Ц( 1 - v 2 / c 2 ) и v z / Ц( 1- v 2 / c 2 ) представляют t -, у- и z-компоненты 4-скорости u m . Компоненты же Е и В входят в электромагнитный тензор вто­рого ранга F m v . Отыскав в табл. 26.1 компоненты F m v , соответ­ствующие Е х , В г и В v , получим

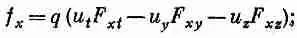
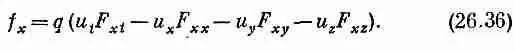
здесь уже начинает вырисовываться что-то интересное. В каж­дом слагаемом есть индекс х, и это разумно, ибо мы находим х-компоненту силы. Все же остальные индексы появляются в парах tt , yy , zz — все, кроме слагаемого с хх, которое куда-то делось. Давайте просто вставим его и запишем

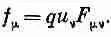
Этим мы ничего не изменили, так как благодаря антисимметрии F m v слагаемое F xx равно нулю. Причиной же нашего желания восстановить его является возможность сокращенной записи уравнения (26.36):

(26.37)

Это по-прежнему уравнение (26.36), если предварительно мы примем соглашение: когда какой-то индекс встречается в произ­ведении дважды (подобно v), нужно автоматически суммировать все слагаемые с одинаковыми значениями этого индекса точно так же, как и в скалярном произведении, т. е. пользуясь тем же самым правилом знаков.

Нетрудно поверить, что уравнение (26.37) так же хорошо работает и для m=y, и для m = z . Но как обстоит дело с m=t? Посмотрим для забавы, что дает формула

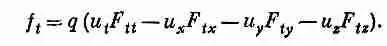
Теперь мы снова должны перейти к Еи В. После этого получается

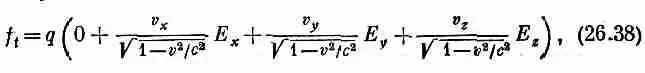
или

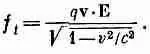
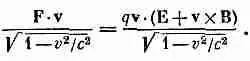
Но в (26.28) f t бралось равным

А это одно и то же, что (26.38), ибо v·(vXB) равно нулю. Так что все идет как нельзя лучше.

В результате наше уравнение движения записывается в элегантном виде:

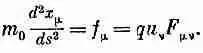
(26.39)

Как ни приятно видеть столь красиво записанное уравнение, форма эта не особенно полезна. При нахождении движения частицы обычно удобнее пользоваться первоначальным урав­нением (26.24), что мы и будем делать в дальнейшем.

*Штрих используется здесь для обозначения запаздывающего поло­жения и времени; не путайте его со штрихом в предыдущей главе, обозначавшим систему отсчета, подвергнутую преобразованиям Лоренца.

* В этом параграфе мы не будем принимать с за единицу.

Глава 27

ЭНЕРГИЯ ПОЛЯ И ЕГО ИМПУЛЬС

§ 1. Локальные законы сохранения

§ 2. Сохранение энергии и электромагнитное поле

§ 3. Плотность энергии и поток энергии в электромагнитном поле

§ 4. Неопределенность энергии поля

§ 5. Примеры потоков энергии

§ 6. Импульс поля

§ 1. Локальные законы сохранения

То, что энергия вещества не всегда сохра­няется, ясно как день. При излучении света объект теряет энергию. Однако потерянную энергию можно представить в какой-то другой форме, скажем, в форме энергии света. Поэтому закон сохранения энергии не полон, если не рассмотреть энергию, связанную со светом, в частности, и с электромагнитным полем вооб­ще. Сейчас мы подправим его, а заодно и закон сохранения импульса с учетом электромагнит­ного поля. Мы, разумеется, не можем обсуждать их порознь, ибо, согласно теории относитель­ности, это различные проявления одного и того же четырехвектора.