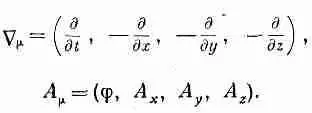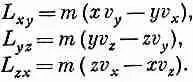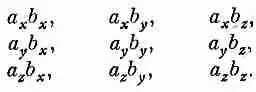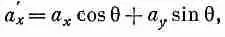Feynmann - Feynmann 6a

Чтобы записать члены F в общем виде, мы воспользуемся обобщенными индексами m и v, каждый из которых может быть 0, 1, 2 или 3, обозначающих соответственно (как и в обычных четырехвекторах) t , x , у или z. Кроме того, все будет прекрасно согласовываться с нашими четырехмерными обозначениями, если F m v определить как

F m v=С mA v-С vA m, (26.19)

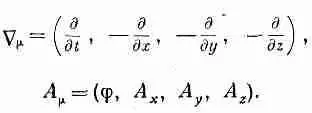
помня при этом, что

То, что мы нашли, можно сформулировать так: в природе су­ществуют шесть величин, которые представляют различные сто­роны чего-то одного. Электрическое и магнитное поля, кото­рые в нашем обычном медленно движущемся мире (где нас не беспокоит конечность скорости света) рассматривались как со­вершенно отдельные векторы, в четырехмерном пространстве уже не будут ими. Они — часть некоторой новой «штуки».

Наше физическое «поле» на самом деле шестикомпонентный объект F m v . Вот как обстоит дело в теории относительности. По­лученные результаты для F m v собраны в табл. 26.1.

Таблица 26.1 · компоненты f m v

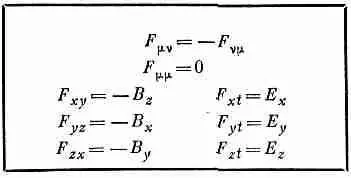
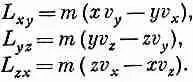
Вы видите, что мы сделали фактически обобщение векторного произведения. Мы начали с ротора и с того факта, что его свой­ства преобразования в точности такие же, как свойства преобра­зования двух векторов — обычного трехмерного вектора А и оператора градиента, который, как нам известно, ведет себя подобно вектору. Возвратимся на минуту к обычному вектор­ному произведению в трехмерном пространстве, например к мо­менту количества движения частицы. При движении частицы в плоскости важной характеристикой оказывается комбина­ция ( xv y — yv x ), а при движении в трехмерном пространстве появляются три подобные величины, которые мы назвали мо­ментом количества движения:

Затем (хотя сейчас вы, может быть, об этом и забыли) мы сотво­рили в гл. 20 (вып. 2) чудо: эти три величины превратились в компоненты вектора. Чтобы сделать это, мы приняли искус­ственное соглашение: правило правой руки. Нам просто повезло. И повезло потому, что момент L tj ( i и j равны х, у или z) ока­зался антисимметричным объектом, т. е.

L ij = - L ji , L ii =0.

Из девяти возможных его величин независимы лишь три. И вот оказалось, что при изменении системы координат эти три опе­ратора преобразуются в точности, как компоненты вектора.

То же свойство позволяет записать в виде вектора и элемент поверхности. Элемент поверхности имеет две части, скажем dx и dy , которые можно представить вектором da , ортогональным к поверхности. Но мы не можем сделать этого же для четырех измерений. Что будет нормалью к элементу dxdy ? Куда она направлена — по оси z или по t ?

Короче говоря, для трех измерений оказывается, что ком­бинацию двух векторов типа L ij , к счастью, снова можно пред­ставить в виде вектора, поскольку возникают как раз три члена, которые, выходит, преобразуются подобно компонен­там вектора. Для четырех измерений это, очевидно, невоз­можно, поскольку независимых членов шесть, а шесть ве­личин вы никак не представите в виде четырех.

Однако даже в трехмерном пространстве можно составить такую комбинацию векторов, которую невозможно представить в виде вектора. Предположим, мы взяли какие-то два вектора a =(а х , a y , a z ) и b =( b x , b y , b z ) и составили всевозможные различ­ные комбинации компонент типа a x b x , a x b y и т. д. Всего получается девять возможных величин:

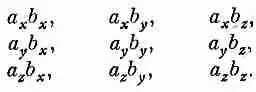
Эти величины можно назвать Т' ij .

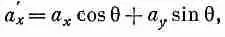
Если теперь перейти в повернутую систему координат (скажем, относительно оси z), то при этом компоненты а и b изменяются. В новой системе а х должно быть заменено на