Feynmann - Feynmann 6a

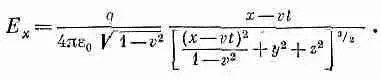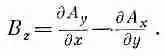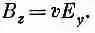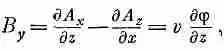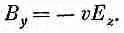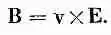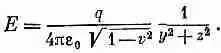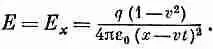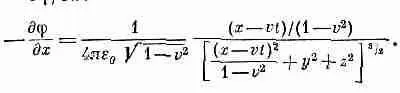
(26.4)

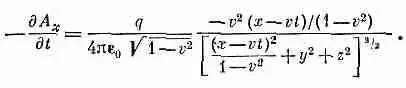
А затем продифференцируем А х по t :

(26.5)

И, наконец, складывая их, получаем

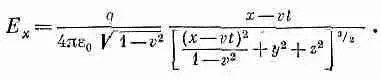
(26.6)

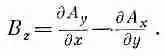
Бросим на минуту заниматься полем Е, а сначала найдем В. Для его z-компоненты мы имеем

Но, поскольку А y равна нулю, у нас остается только одна производная. Заметьте, однако, что А х просто равна vj, а производная ( d / dy ) v j равна — vE y . Так что

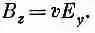
(26.7)

Аналогично,

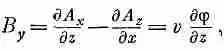
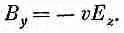
или

(26.8)

Наконец, компонента В х равна нулю, поскольку равны нулю и А у и А г . Таким образом, магнитное поле можно запи­сать в виде

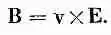
(26.9)

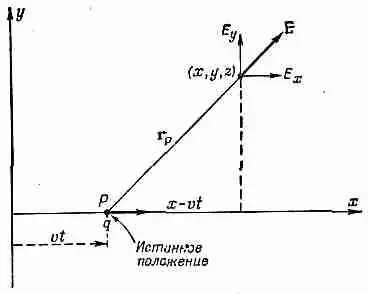
Теперь посмотрим, как выглядят наши поля. Мы попытаемся нарисовать картину поля вокруг положения заряда в настоящий момент. Конечно, влияние заряда в каком-то смысле происхо­дит из запаздывающего положения, но, поскольку мы имеем дело со строго заданным движением, запаздывающее положение однозначно определяется положением в настоящий момент. При постоянной скорости заряда поля лучше связывать с теку­щими координатами, ибо компоненты поля в точке х, у, z за­висят только от (х - vt ), у и z, которые являются компонентами вектора перемещения r p из постоянного положения заряда в точку (х, у, z ) (фиг. 26.3).

Фиг. 26.3. Электрическое поле заряда, движущегося с постоянной скоростью, направ­лено по радиусу от истинного положения заряда.

Рассмотрим сначала точки, для которых z= 0. Поле Е в этих точках имеет только х- и y-компоненты. Из уравнений (26.3) и (26.6) видно, что отношение этих компонент как раз равно отно­шению х- и y-компонент вектора перемещения. Это означает, что направление Е совпадает с направлением r p , как это пока­зано на фиг. 26.3. Тот же результат остается справедливым и для трех измерений, поскольку E z пропорционально z. Короче говоря, электрическое поле заряда радиально и силовые линии расходятся от заряда так же, как и в стационарном случае. Конечно, вследствие наличия дополнительного фактора (1-v 2 ) поле не будет тем же самым, что в стационарном случае. Но здесь мы можем увидеть нечто очень интересное. Дело обстоит так, как будто вы пишете закон Кулона в особой системе коорди­нат, «сжатой» вдоль оси x множителем Ц(1-v 2) Если вы сделаете это, то силовые линии впереди и позади заряда разойдутся, а по бокам сгустятся (фиг. 26.4).

Если мы связываем обычным образом напряженность поля Е с плотностью силовых линий, то видим, что поле впереди и по­зади заряда ослабевает, но зато по бокам становится сильнее, т. е. как раз то, о чем говорит нам уравнение. Когда вы изме­ряете напряженность поля под прямыми углами к линии дви­жения, т. е. при (x - vt ) = 0, расстояние от заряда будет равно y 2+z 2, а полная напряженность Ц( E 2 x + E 2 y ) в этих точках равна

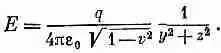
(26.10)

Она, как и в случае кулонова поля, пропорциональна квад­рату расстояния, но еще усиливается постоянным множителем 1/Ц(1-v 2), который всегда больше единицы. Таким образом, по бокам движущегося заряда электрическое поле сильнее, чем это следует из закона Кулона. Фактически увеличение по срав­нению с кулоновым потенциалом равно отношению энергии частицы к ее массе покоя.

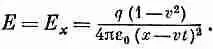
Впереди заряда (или позади него) у и z равны нулю, а поэ­тому

(26.11)