* В английском оригинале « unworldliness ». — Прим. ред.
Глава 26
ЛОРЕНЦЕВЫ ПРЕОБРАЗОВАНИЯ ПОЛЕЙ
§ 1. Четырехмерный потенциал движущегося заряда
§ 2. Поля точечного заряда, движущегося с постоянной скоростью
§ 3. Релятивистское преобразование полей
§ 4. Уравнение движения в релятивистских обозначениях
В этой главе c=1
Повторить: гл. 20 «Решение уравнений Максвелла в пустом пространстве»
§ 1. Четырехмерный потенциал движущегося заряда
В предыдущей главе мы видели, что потенциал A m=(j, А) является четырехвектором. Его временной компонентой служит скалярный потенциал j, а тремя пространственными компонентами— векторный потенциал А. Используя преобразования Лоренца, мы нашли также потенциал частицы, движущейся прямолинейно с постоянной скоростью. (В гл. 21 то же самое было сделано несколько иным методом.) Для точечного заряда, координаты которого в момент t равны ( vt , 0, 0), потенциалы в точке (х, у, z ) имеют вид
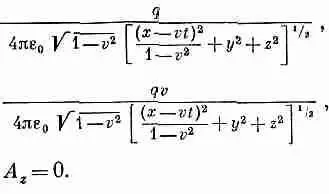
(26.1)
Уравнения (26.1) дают потенциалы в точке х, у, z в момент t , возникающие от движущегося заряда, «истинное» положение которого (имеется в виду положение в момент времени t ) x = vt . Заметьте, что в уравнение входят координаты (x- vt ), у и z , которые являются координатами относительно переменного положения Р движущегося заряда (фиг. 26.1). Но, как вы знаете, истинное влияние распространяется на самом деле со скоростью с, так что поле в точке определяется на самом деле запаздывающим положением заряда Р', координата х которого равна vt ' (где t '= t - r '/с — «запаздывающее» время».)
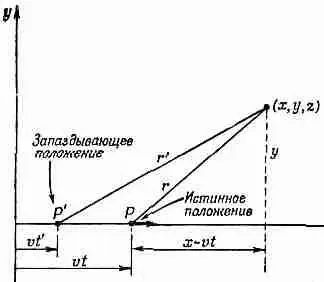
Фиг. 26.1. Определение полей в точке P от заряда q , движущегося вдоль оси x с постоянной скоростью v . (Поле в точке ( x , y , z ) в «настоящий момент» можно выразить как через «истинное» положение P так и через «запаздывающее» положение P ’ ( т. е. положение в момент t ’= t - r ’/ c ).
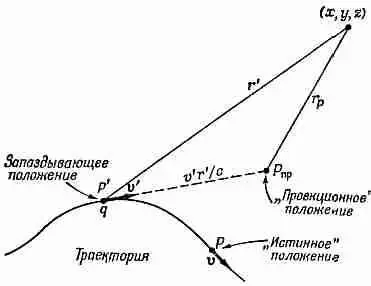
Нам, однако, известно, что заряд двигался с постоянной скоростью по прямой линии, поэтому естественно, что поведение в точке Р' непосредственно связано с переменным положением заряда. Фактически, если мы добавим предположение, что потенциалы зависят только от положения и скорости в запаздывающий момент, тогда уравнение (26.1) будет представлять собой полную формулу для потенциалов заряда, движущегося любым образом. Вот как все это работает. Пусть у вас имеется заряд, движущийся каким-то произвольным образом, скажем, по траектории, изображенной на фиг. 26.2, и вы пытаетесь найти потенциал в точке (х, у, z ). Прежде всего вы находите запаздывающее положение Р' и скорость v ' в этой точке. Вообразите затем, что заряд сохраняет свое движение с этой скоростью на весь период запаздывания ( t '- t ), так что он появился бы затем в воображаемом положении Р пр, которое мы будем называть «проекционным», причем двигаясь с той же скоростью v '. (На самом деле он, конечно, не делает этого; в момент t он находится в точке Р.) Тогда потенциалы в точке (х, у, z ) будут как раз такими, которые дали бы уравнения (26.1) для воображаемого заряда в проекционном положении Р пр. Мы хотим здесь сказать, что, поскольку потенциалы зависят только от того, что делает заряд в запаздывающий момент, они будут одинаковы, независимо от того, продолжает ли заряд свое движение с постоянной скоростью или изменяет его после момента t' , т. е. после того, как потенциалы, которые возникнут в момент t в точке (х, у, z ), уже определены.
Вы понимаете, конечно, что в тот момент, когда получены формулы для потенциалов произвольно движущегося заряда, мы имеем полную электродинамику; из принципа суперпозиции мы можем получить потенциалы для любого распределения зарядов.
Читать дальше