Feynmann - Feynmann 4

Рассмотрим движущуюся частицу, которая проходит рас­стояние dx внутри газа, содержащего n 0 рассеивателей (молекул) в единичном объеме (фиг. 43.1).

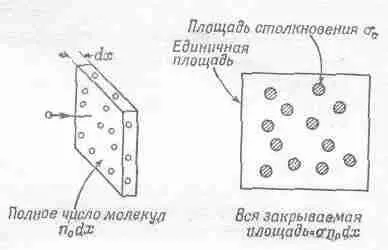
Фиг. 43,1. Эффективное сечение столкновения.

На каждой площадке единичной площади, перпендикулярной к направлению движения вы­бранной нами частицы, имеется n 0 dx молекул. Если каждая может быть представлена эффективной площадью столкновения, или, как обычно говорят, «эффективным сечением столкно­вения» s с , то полная площадь, покрываемая рассеивателями, равна s c n 0 dx .

Под «эффективным сечением столкновения» понимается площадь, в которую должен попасть центр частицы, если она должна столкнуться с заданной молекулой. Если моле­кулы выглядят как маленькие шарики (классическая кар­тина), то следует ожидать, что s с = p ( r 1 + r 2 ) 2 , где r 1 и r 2 — радиусы двух сталкивающихся молекул. Вероятность того, что наша частица столкнется с какой-нибудь молекулой, равна отношению площади, покрываемой рассеивающими молеку­лами, к полной площади, принятой нами за единицу. Та­ким образом, вероятность столкновения на пути dx равна s с n 0 dx :

Вероятность столкновения на пути dx = s n 0 dx . (43.10)

Мы уже отметили раньше, что вероятность столкновения на пути dx может быть записана в терминах длины свобод­ного пробега l как dx / l . Сравнивая это с (43.10), можно связать длину свободного пробега с эффективным сечением столкновения:

1/l= s cn 0. (43.11)

Это равенство легче запомнить, если записать его так:

s с n 0 l = 1. (43.12)

Эта формула говорит, что если частица проходит путь I внутрь рассеивателя, в котором молекулы могут как раз покрыть всю площадь, то в среднем происходит одно столк­новение. В цилиндре высотой l , поставленном на основание единичной площади, содержится n 0 l рассеивателей; если каж­дый из них занимает площадь s с, то полная площадь, покрытая ими, равна n 0 l s c , а это как раз единичая площадь. Конечно, молекулы не покрывают всей площади целиком, потому что часть молекул прячется за соседние молекулы. Поэтому не­которые молекулы пройдут между столкновениями большее, чем l , расстояние. Ведь это только в среднем молекулам между столкновениями дается ровно столько времени, чтобы они смогли пройти расстояние l . Измеряя длину свободного про­бега l , можно определить эффективное сечение рассеяния s c и сравнить этот результат с расчетами, основанными на де­тальной теории строения атомов. Но это уже совсем другая тема! А пока вернемся к проблеме неравновесных состояний.

§ 3. Скорость дрейфа

Мы хотим описать поведение одной или нескольких молекул, которые чем-то отличаются от огромного большинства осталь­ных молекул газа. Будем называть «большинство» молекул молекулами «фона», а отличающиеся от них молекулы получат название «особых» молекул, или (для краткости) S-молекул. Молекула может быть особой по целому ряду причин: она может быть, скажем, тяжелее молекул фона. Может она отли­чаться от них также химическим составом. А, может быть, особые молекулы несут электрический заряд — тогда это будет ион на фоне нейтральных молекул. Из-за необычности масс или зарядов на S-молекулы действуют силы, отличающиеся от сил между молекулами фона. Изучая поведение S-молекул, можно понять основные эффекты, которые вступают в игру во многих разнообразных явлениях. Перечислим некоторые из них: диффузия газов, электрический ток в батарее, осаждение, разделение при помощи центрифуги и т. д.

Начнем с изучения основного процесса: на S-молекулу в газе из молекул фона действуют какая-то особая сила F(это может быть сила тяжести или электрическая сила) и, кроме того, более обычные силы, обусловленные столкновениями с молекулами фона. Нас интересует общий характер поведения S-молекулы. Детальное описание ее поведения — это непре­рывные стремительные удары и следующие одно за другим столкновения с другими молекулами. Но если проследить внимательно, то станет ясно, что молекула неуклонно движется по направлению силы F. Мы говорим, что дрейф накладывается на беспорядочное движение. Но нам хотелось бы знать, как зависит скорость дрейфа от силы F.