Нихиль Будума - Основы глубокого обучения

Один из вариантов выражения дерева в виде последовательности — линеаризация. Рассмотрим примеры на рис. 7.6. Если у вас есть граф с корнем R и дочерними элементами А (связаны ребром r_a), B (связаны ребром r_b) и C (связаны ребром r_c), можно выполнить линейное преобразование, получив (R, r_a, A, r_b, B, r_c, C). Так легко представить и более сложные графы. Допустим, у узла B есть еще два дочерних элемента: D (ребро b_d) и E (ребро b_e). Этот новый граф можно представить как (R, r_a, A, r_b, [B, b_d, D, b_e, E], r_c, C).

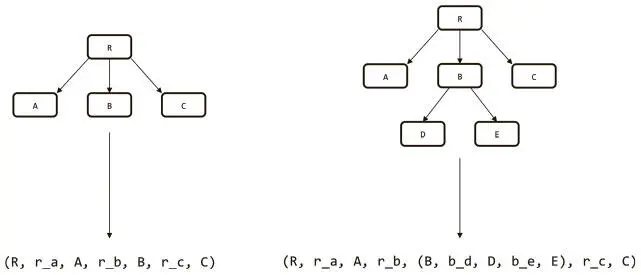
Рис. 7.6. Пример линейного преобразования двух деревьев. Для удобства чтения на диаграммах не подписаны ребра

В той же парадигме мы можем выполнить линейное преобразование нашего примера разбора зависимости, как показано на рис. 7.7.

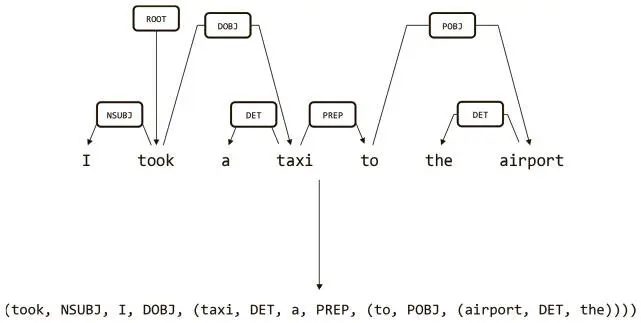
Рис. 7.7. Линейное преобразование примера дерева разбора зависимостей

Одна из интерпретаций этой проблемы seq2seq — чтение предложения ввода и получение на выходе последовательности знаков, представляющей собой линейное преобразование разбора зависимостей входящих данных. Но не до конца понятно, как реализовать здесь ту же стратегию, что и в предыдущем разделе, если там существовала четкая привязка слов к меткам частей речи. Более того, там мы могли легко принимать решения о метке для части речи на основе ближайшего контекста. При разборе зависимостей нет четкой связи между расположением слов в предложении и символов в его линейном представлении. И, судя по всему, при разборе зависимостей придется определять ребра, которые могут относиться ко множеству слов. На первый взгляд кажется, будто схема прямо противоречит изначальному заявлению о том, что нам не нужно учитывать долгосрочные связи.

Чтобы упростить решение, можно переосмыслить задачу разбора зависимостей как попытку поиска последовательности верных «действий», которая генерирует корректный разбор. Эта техника получила название системы стандартных дуг , была впервые описана в 2004 году Иоакимом Нивром [84], а затем применена в контексте нейросетей Данки Ченом и Кристофером Мэннингом в 2014 году [85].

В системе стандартных дуг мы сперва помещаем в стек первые два слова предложения, а оставшиеся сохраняем в буфере, как показано на рис. 7.8.

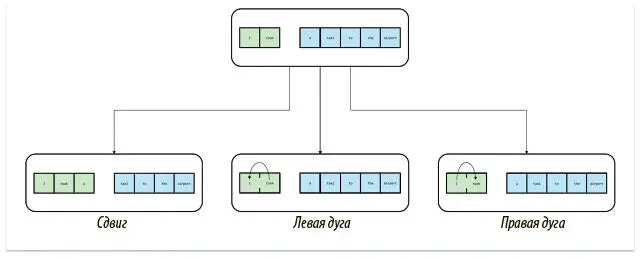
Рис. 7.8. На каждом шаге у нас три варианта: передвинуть слово из буфера (голубого) в стек (зеленый), провести дугу от правого элемента к левому (левая дуга) или от левого к правому (правая дуга)

На каждом шаге мы можем выполнить одно из трех действий.

СДВИГ

Передвинуть слово из буфера в переднюю часть стека.

ЛЕВАЯ ДУГА

Объединить два элемента в передней части стека в общую единицу, где корень правого элемента будет родительским узлом, а левого — дочерним.

ПРАВАЯ ДУГА

Объединить два элемента в передней части стека в общую единицу, где корень левого будет родительским узлом, а правого — дочерним.

И если СДВИГ можно выполнить только одним способом, то ДУГИ могут осуществляться разными методами в соответствии с ярлыками зависимости, назначаемыми результату. Но мы упростим изложение и иллюстрации в этом разделе и будем считать, что каждое решение — выбор из трех действий (а не нескольких десятков).

Мы заканчиваем процесс, когда буфер пустеет, а в стеке остается один элемент, представляющий полный разбор зависимостей. Чтобы проиллюстрировать процесс, рассмотрим на рис. 7.9 пример последовательности действий, которые создают разбор зависимостей для нашего входного предложения.

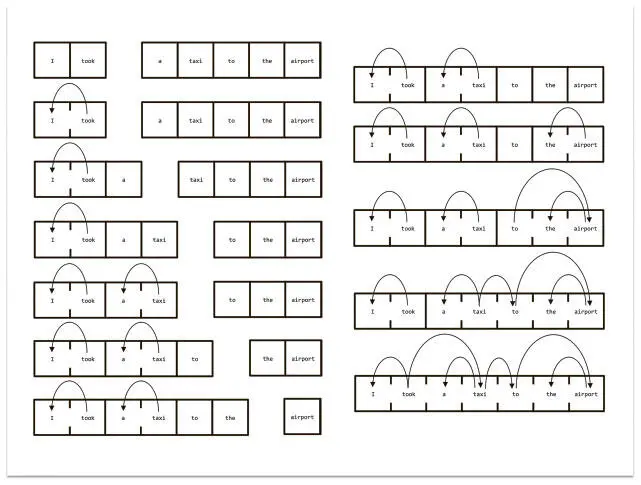
Рис. 7.9. Последовательность действий, которые ведут к корректному разбору зависимостей (ярлыки опускаем)

Не так сложно переформулировать эту принимающую решения схему в виде проблемы обучения. На каждом шаге мы берем текущую конфигурацию и преобразуем ее в векторный вид, извлекая множество описывающих ее признаков (слов в определенных местах стека/буфера, дочерних элементов слов в этих местах, меток частей речи и т. д.).

Во время обучения мы можем ввести этот вектор в сеть с прямым распространением сигнала и сравнить ее предсказания последующих действий с «золотым стандартом» решений, принимаемых лингвистом-человеком.