Нихиль Будума - Основы глубокого обучения

В предыдущих главах эта идея не рассматривалась. Сети с прямым распространением сигнала по природе своей не имеют «состояний». После обучения любая из них становится статичной. Она не может ни переключать память между разными входными данными, ни изменять способы их обработки на основе входных данных, с которыми имела дело в прошлом. Чтобы реализовать эту стратегию, придется пересмотреть архитектуру нейронных сетей и начать создавать модели глубокого обучения с фиксацией состояния. Вернемся к рассмотрению сетей на уровне нейронов. В следующем разделе поговорим о том, как рекуррентные связи (в отличие от прямых, которые мы рассматривали ранее) позволяют моделям фиксировать состояние, и опишем класс моделей, известных как рекуррентные нейронные сети (РНС) .

Первые РНС были предложены в 1980-е годы, но популярность обрели лишь недавно благодаря нескольким интеллектуальным и техническим прорывам, которые помогли повысить их обучаемость. РНС отличаются от сетей с прямым распространением сигнала, потому что в них используется особый тип нейронного слоя, именуемый рекуррентным и позволяющий сети сохранять свое состояние в промежутках между сеансами ее использования.

На рис. 7.14 показана нейронная архитектура рекуррентного слоя. У всех нейронов есть входные соединения, приходящие от всех нейронов предыдущего слоя, и выходные, ведущие ко всем нейронам последующего. Однако эти типы соединений для рекуррентного слоя не единственные. В отличие от слоя с прямым распространением сигнала, он обладает рекуррентными соединениями, которые распространяют информацию между нейронами одного слоя. В полносвязном подобном слое информационный поток идет от каждого нейрона к каждому нейрону того же слоя (в том числе и к себе). У такого слоя с числом нейронов r есть r 2 рекуррентных соединений.

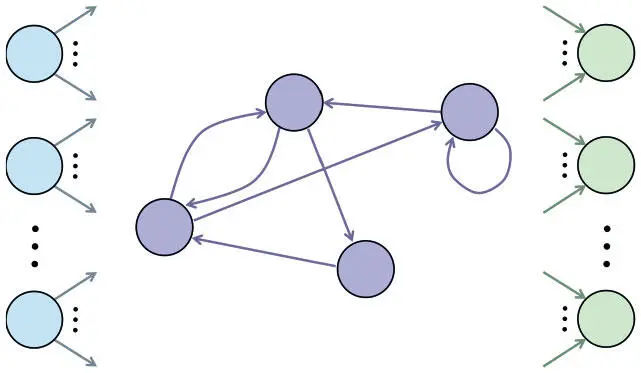
Рис. 7.14. Рекуррентный слой содержит рекуррентные соединения между нейронами, расположенными на одном уровне

Чтобы лучше понять, как работает РНС, рассмотрим ее функционирование после соответствующего обучения. Каждый раз, когда нам нужно обработать очередную последовательность, мы создаем новый экземпляр нашей модели.

Можно работать с сетями, содержащими рекуррентные слои, разделив срок жизни экземпляра сети на дискретные временные шаги. На каждом шаге мы вводим в модель следующий элемент данных. Прямые соединения отражают информационный поток от одного нейрона к другому, в котором передаваемые данные — подсчитанная нейронная активация на текущем шаге. В случае же рекуррентных связей данные — сохраненная нейронная активация на предыдущем шаге. Таким образом, активации нейронов здесь отражают накапливаемое состояние экземпляра сети. Изначальные активации нейронов в рекуррентном слое — параметры нашей модели, и их оптимальные значения мы определяем точно так же, как лучшие значения для весов каждого соединения в процессе обучения. Оказывается, при фиксированном времени жизни (например, t шагов) экземпляра РНС мы можем выразить его в виде сети с прямым распространением сигнала, хоть и с нерегулярной структурой.

Это хитрое преобразование, показанное на рис. 7.15, часто именуется «разворачиванием» РНС во времени. Рассмотрим экземпляр РНС на рисунке. Нам нужно связать последовательность двух входов (каждый — размера 1) с одним выходом (тоже размера 1). Это преобразование мы осуществляем, взяв нейроны одного рекуррентного слоя и скопировав их t раз — по разу для каждого шага. Точно так же мы воспроизводим нейроны входного и выходного слоев. С каждым шагом мы копируем и прямые связи — такими, какими они были в исходной сети. Затем мы воссоздаем рекуррентные связи в виде прямых от каждой временной копии к следующей (поскольку такие связи отражают нейронную активацию предыдущего временного шага).

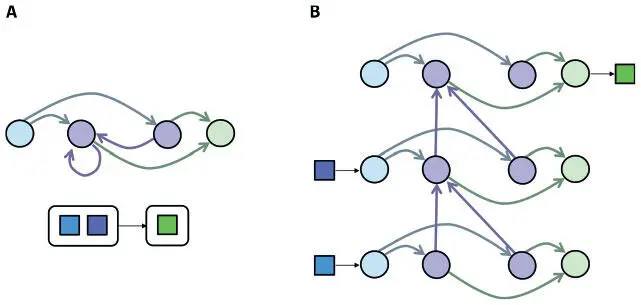
Рис. 7.15. Мы можем развернуть РНС во времени, чтобы выразить ее в виде сети с прямым распространением сигнала, которую можно обучить с помощью алгоритма обратного распространения ошибок

Теперь мы можем обучить РНС, вычислив градиент для развернутой версии. Это значит, что все алгоритмы обратного распространения ошибок, которые использовались для сетей с прямым распространением сигнала, подойдут и для РНС. Но есть одна проблема. После каждого пакета обучающих примеров необходимо изменить веса на основании вычисленных производных ошибок. В развернутой сети у нас есть наборы связей, и все они соответствуют одной связи из исходной РНС. А вот производные ошибок для этих развернутых связей не обязательно будут равны (на практике они чаще всего и не равны). Можно обойти эту проблему, усреднив или суммировав производные ошибок для всех связей одного набора. Это позволит использовать производную ошибок, учитывающую всю действующую на веса соединения динамику, при попытке заставить сеть выдать точный результат.