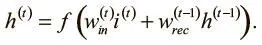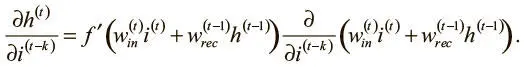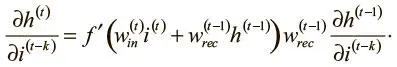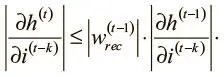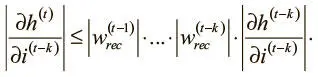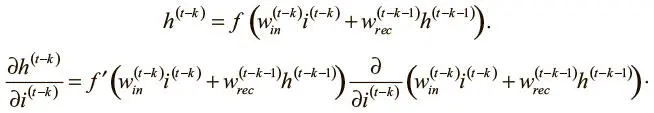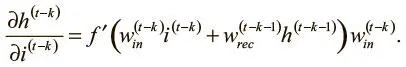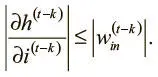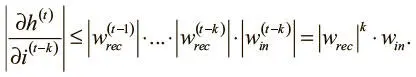Нихиль Будума - Основы глубокого обучения

Мотивы использования модели сети с фиксацией состояния связаны с идеей отражения долгосрочных зависимостей во входной последовательности. Вроде бы логично предположить, что РНС с большим банком памяти (рекуррентным слоем значительного размера) сможет запомнить все эти зависимости. И действительно, теоретически еще в 1996 году Джо Килиан и Хава Сигельманн показали, что РНС — универсальное функциональное представление [89]. Иными словами, при достаточном количестве нейронов и правильной настройке параметров РНС можно использовать для представления любых функциональных зависимостей между входными и выходными последовательностями. Эта теория много обещает, но на практике реализуется не всегда. Хоть и полезно знать, что РНС может выразить любую произвольную функцию, лучше понимать, насколько практически полезно с нуля обучать ее реалистическим функциональным связям путем применения алгоритмов градиентного спуска. Если это непрактично, мы окажемся в затруднительном положении, так что рассмотреть вопрос нужно максимально строго. Начнем с анализа самой простой РНС из возможных (рис. 7.16): один входной нейрон, один выходной, полносвязный рекуррентный слой тоже с одним нейроном.

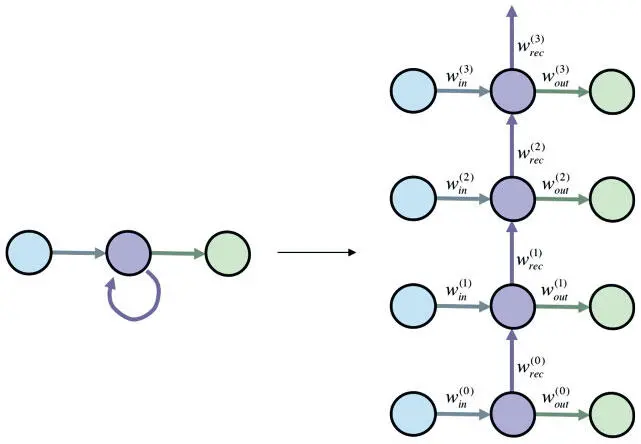
Рис. 7.16. Один нейрон в полносвязном рекуррентном слое (в сжатом и развернутом во времени видах) — пример анализа обучающих алгоритмов на основе градиента

Начнем с простого. При нелинейности f мы можем выразить активацию h (t) скрытого нейрона рекуррентного слоя на шаге t следующим образом, где i (t) — входной логит входного нейрона на временном шаге t :

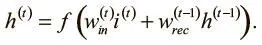
Попытаемся вычислить, как активация скрытого нейрона будет меняться в ответ на корректировки входящего логита в течение k шагов в прошлом. Анализ этого компонента градиентных выражений обратного распространения ошибок начнем с оценки того, сколько «памяти» сохраняется от предшествующих входных данных.

Сначала возьмем частную производную и применим правило дифференцирования сложной функции:

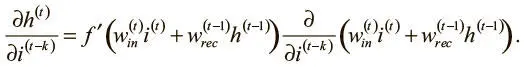
Поскольку значения весов входного и рекуррентного соединений не зависят от входного логита на временном шаге ( t − k), можно упростить выражение:

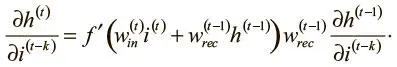
Поскольку нам интересна величина этой производной, можно взять абсолютное значение обеих сторон. Мы также знаем, что для всех обычных нелинейностей (гиперболического тангенса — tanh, логистической и ReLU) максимальное значение f ′ равно 1. Отсюда выводим следующее рекурсивное неравенство:

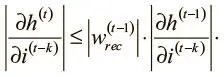
Можно продолжить рекурсивно расширять его, пока не дойдем до основного случая на шаге ( t − k):

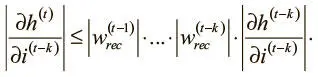
Оценить эту частную производную можно уже рассмотренным путем:

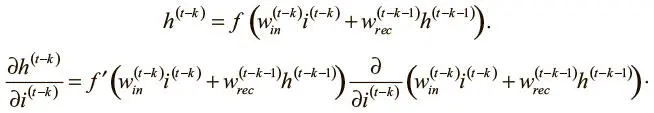
В этом выражении активация скрытого слоя на шаге ( t − k − 1) не зависит от значения входных данных на шаге ( t − k).

Поэтому мы можем переписать его:

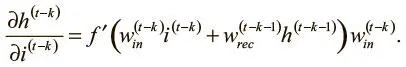
Наконец, взяв абсолютное значение для обеих сторон и вновь применив наблюдение относительно максимального значения f ′, можно записать:

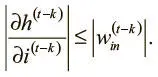
В результате получаем итоговое неравенство (которое можно упростить, поскольку мы хотим, чтобы связи на разных шагах имели одинаковые значения):

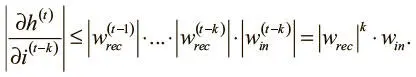
Это отношение устанавливает жесткую верхнюю границу того, как изменения во входных данных на шаге ( t − k) влияют на скрытое состояние на шаге t . Поскольку веса нашей модели в начале обучения невелики, значение этой производной с возрастанием k стремится к 0. Иными словами, градиент быстро уменьшается, когда он вычисляется по входным данным на несколько шагов назад, что существенно ограничивает способность модели к изучению долгосрочных зависимостей. Эта проблема обычно называется проблемой исчезающего градиента . Она серьезно влияет на способности обычных рекуррентных нейронных сетей к обучению. Наша задача — устранить эти ограничения, и в следующем разделе мы поговорим о чрезвычайно эффективном подходе к рекуррентным слоям, который именуется долгой краткосрочной памятью.