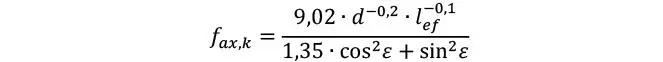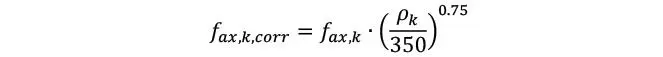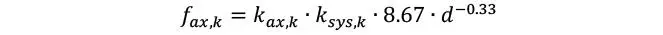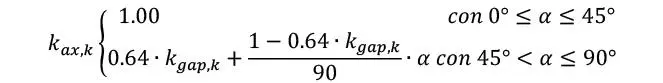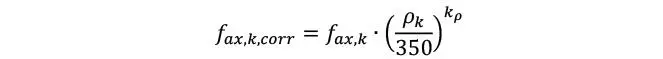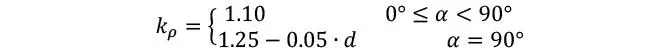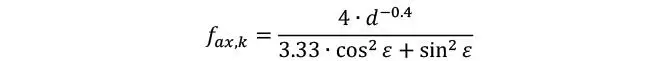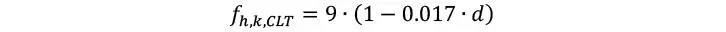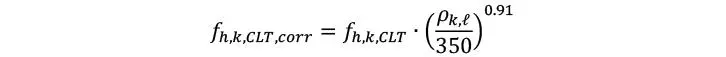Pablo Guindos - Conceptos avanzados del diseño estructural con madera

1.5.8.1 Capacidad de extracción axial

Más allá de aprobaciones técnicas para productos específicos, no existen ecuaciones específicas en la normativa para determinar la capacidad axial de conectores en el CLT. Sin embargo, a continuación, se sugiere el empleo de ecuaciones diferenciadas ya que, por lo general, la capacidad axial de los conectores puede ser inferior en el CLT en comparación a la madera maciza o laminada, especialmente cuando estos son insertados en los bordes, debido a la presencia de huecos y ranuras tal como se detalló en la sección anterior.

Extracción axial de tornillos autoperforantes

Se recomienda el empleo de la ecuación de Blab y Uibel (2015), para cuando los tornillos son insertados de forma perpendicular a las caras o bordes del CLT (i.e. α = 90°).

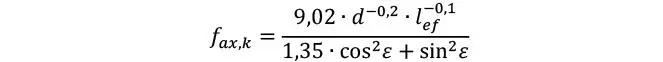
Donde d es el diámetro, lef es la longitud efectiva de anclaje, y e toma en cuenta si es que el tornillo es insertado en las caras (ε = 90°) o los bordes (ε = 0°) del CLT; se observa por tanto que la resistencia axial decrece considerablemente, cuando el tornillo se inserta en los bordes por mayor riesgo de huecos o ranuras. Posteriormente se recomienda corregir la resistencia axial según la densidad característica del CLT

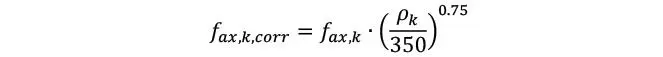
La cual, debería determinarse a partir de la densidad característica de las propias laminaciones como

Como puede verse en la ecuación anterior, en la práctica europea la densidad se mayora un 10% para conectores situados en las caras del CLT, por el hecho de que forzosamente van a atravesar más de una laminación, por lo que la posibilidad de obtener un valor bajo de densidad es muy inferior a los conectores en los bordes, los cuales mayormente atraviesan una única laminación.

En caso de disponer tornillos oblicuos, se recomienda la ecuación de Ringhofer et al. (2013)

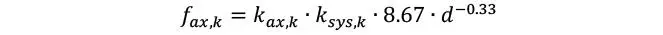
Donde ksys,k es un factor de mayoración que toma en cuenta la redundancia de distintas laminaciones (y por tanto la posibilidad de tener una capacidad superior a la característica), y toma un valor de 1,1 para CLT (1 si la ecuación se aplicase a madera maciza, y 1.13 si fuese MLE con 5 o más laminaciones). Por otra parte el ángulo de inserción se toma en cuenta con

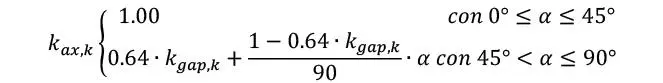
Finalmente, la consideración de inserción o caras o bordes se toma en cuenta con

Finalmente, la corrección por densidad es similar al modelo de tornillos no oblicuos

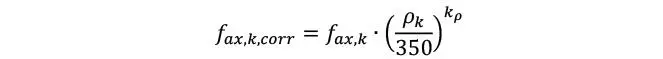
Solo que el ángulo α también interviene en la corrección

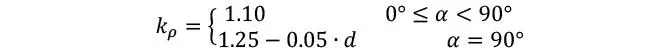
Extracción axial de clavos corrugados

Se propone la ecuación de Blab y Uibel (2015), la cual es muy similar a la de los tornillos autoperforantes solo que el efecto de borde (diferencia de capacidad por inserción en bordes) es mucho más pronunciado debido al menor diámetro de los clavos, ver Figura 1.5.8.1.

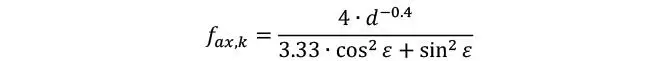
con

Se recomienda aplicar esa ecuación únicamente con d≥4 mm, y lef≥8d, además si d<6 se debe minorar la capacidad multiplicando por 0,8.

FIGURA 1.5.8.1 Efecto de extracción axial en bordes del CLT según el modelo de Blass y Uibel (basado en Schickhofer et al. 2009).

1.5.8.2 Capacidad de aplastamiento lateral

Aplastamiento lateral de pasadores y pernos

La situación regulatoria es similar a la de la capacidad axial. Para conectores insertados en las caras, se sugiere la ecuación de Blab y Uibel (2015), la cual es bastante parecida a la ecuación del EC5 correspondiente a la madera maciza y MLE, solo que la influencia del ángulo fuerza-fibra de la capa externa (β) es bastante menor

con

Tal como se ilustra en la Figura 1.5.8.2.1, la capacidad de aplastamiento en caras del CLT es ligeramente inferior a la MLE o madera maciza, especialmente para densidades bajas y diámetros pequeños por el efecto de los huecos y las ranuras; sin embargo, la dispersión por el efecto de la desangulación fuerza-fibra es muy inferior en el CLT por el efecto de refuerzo de las capas transversales.

FIGURA 1.5.8.2.1 Comparación de la capacidad lateral de aplastamiento de pernos y pasadores insertados en caras del CLT en relación a la madera maciza y MLE respecto del CLT. La capacidad es ligeramente inferior para densidades y diámetros pequeños, pero la dispersión por desangulación β es muy inferior en el CLT (modificado de Schickhofer et al. 2009).

Para el caso de que los conectores se inserten en los bordes, la influencia de huecos y en ranuras es mayor, y en general la capacidad es bastante menor que cuando son insertados en las caras. Además, en el caso de inserción en bordes y carga fuera del plano del CLT, existe riesgo de rotura por tracción perpendicular, lo cual se puede atenuar principalmente asegurando que las láminas cumplan con las especificaciones de espesores mínimos de laminación en fabricación. Por todo ello, diversos autores desaconsejan emplear pernos o pasadores para carga lateral en bordes. No obstante, la moderada capacidad en dichas situaciones puede aproximarse con el modelo de Blab y Uibel (2015)

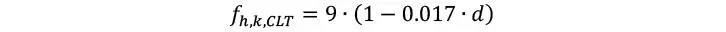
con

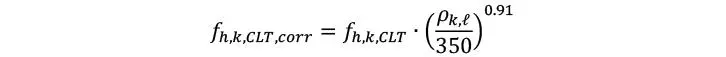
donde en este caso la corrección por densidad es según la densidad característica de la laminación, no el CLT.

Aplastamiento lateral tornillos autoperforantes y clavos corrugados

Para inserción en caras existen pocas evidencias experimentales pero diversos autores recomiendan aplicar las mismas ecuaciones que para madera maciza y MLE.

Para inserción en bordes, se comportan de forma muy parecida a pernos y pasadores; por lo general, no es muy recomendable la inserción en bordes, pero puede predecirse la capacidad con la siguiente ecuación

con

En la Figura 1.5.8.2.2 se ilustra una comparación entre la capacidad lateral de tornillos y clavos corrugados insertados en caras (calculados según el EC5 con las ecuaciones de MLE y madera maciza) y aquellos insertados en bordes calculados según la ecuación anterior. Como puede observarse en la figura, la capacidad en bordes es aproximadamente 1/3 de la capacidad en caras.