Pablo Guindos - Conceptos avanzados del diseño estructural con madera

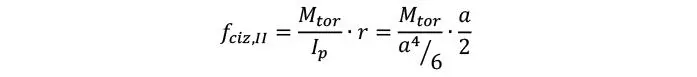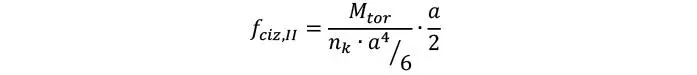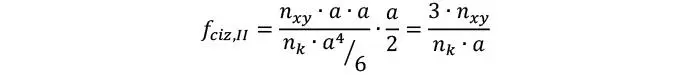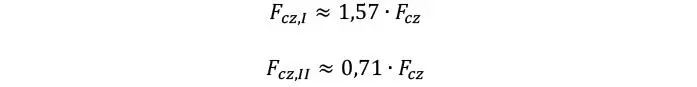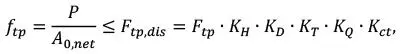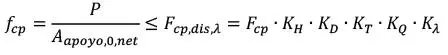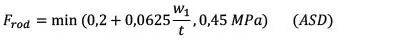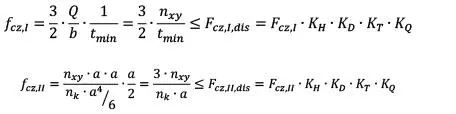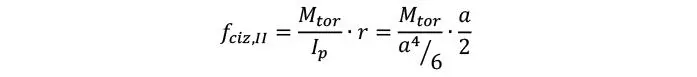
Dado que la torsión se reparte en paralelo por cada superficie de encolado (nk), la tensión de cizalle por torsión se reduce a

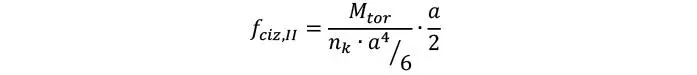
y dado que el momento torsor en el área de cada tablón puede estimarse como nxy ·a · a

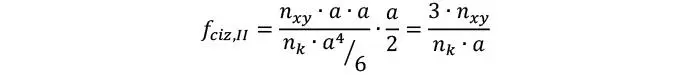
Para el caso de que un panel de CLT sea rectangular (h·b), y esté sometido a un corte horizontal constante V, la solicitación de torsión puede calcularse directamente a partir de la fuerza cortante como

Con ntot = número de “cuadrados” áreas de torsión por solape de tablones en el panel, i.e. ntot = nk· nh · nv, con nh = b/a y nv = h/a.

Ya sea que el panel está sometido a un corte uniforme (V), o bien un flujo de corte unitario no uniforme (nxy), la verificación que debe satisfacerse es

Es importante notar que, si bien en muchas ocasiones el mecanismo II produce una rotura por corte de la madera cercana al adhesivo entre láminas, también es posible que el esfuerzo torsor produzca un fallo por rodadura en los tablones, por lo que algunos autores han propuesto ecuaciones más sofisticadas para la verificación correspondiente al mecanismo II. Por otro lado, debe notarse que aún a día de hoy existen pocos datos experimentales acerca de los valores resistentes, Fcz,I y Fcz,II, especialmente en la literatura norteamericana. Por el momento se recomienda tomar como referencia el caso europeo, donde diversos autores proponen aproximadamente

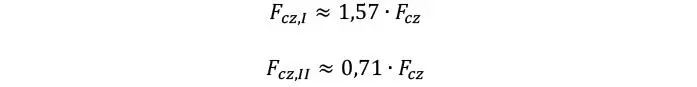
Recuérdese que tal como se detalló en la Sección 1.3.7 la rigidez de corte en el plano se reduce mediante el factor kv, que en la mayoría de ocasiones adopta valores entre 0,6-0,8.

1.4.9 Combinación de esfuerzos

La mayoría de las interacciones de tensiones no se encuentran normalizadas en el CLT, y en la actualidad se asume casi siempre cuál es el tipo de interacción de cada combinación de tensiones basándose en la experiencia con MLE, mientras no se tengan mayores evidencias experimentales. A continuación, se resumen las interacciones que mayormente se consideran en el cálculo analítico. El lector debe notar que las combinaciones tensionales analíticas se encuentran considerablemente menos desarrolladas que las combinaciones típicamente consideradas en los modelos computacionales, por lo que se recomienda consultar primeramente la Sección 1.3.12.

Flexión en el plano y compresión

En Norteamérica se propuso una modificación de la combinación de flexión y compresión amplificada por efectos de segundo orden de vigas-columnas para el caso del CLT

Donde P es el axil de excentricidad e, Pce es la capacidad crítica de pandeo, Fcp,dis,λ es la tensión de diseño considerando pandeo, Aapoyo,0,net es el área resistente a la compresión (ver Sección 1.4.3), Fft,dis es la tensión de diseño en flexión y Wef es el módulo resistente a la flexión efectivo (ver Sección 1.4.5).

Para otras combinaciones de flexión y fuerzas axiales, se recomienda consultar la Sección 1.3.12. La aplicación de principios de vigas compuestas en lo referente a la combinación de esfuerzos axiales y flexionales se detalla en apartados sucesivos.

Flexión biaxial

Cuando un panel está sometido a acciones biaxiales, por ejemplo, cuando un panel soporta acciones gravitacionales y se apoya en 3 o 4 de sus bordes, el cálculo suele hacerse con modelos computacionales de placas tal como se presentó en la Sección 1.3. No obstante, para geometrías y condiciones de apoyo sencillas, el cálculo analítico es factible. En efecto, se considera que la flexión biaxial produce tensiones axiales en diferentes láminas del CLT, ver Figura 1.4.9, por lo que las verificaciones se suelen hacer por separado. Así, si h/b>2, el panel suele calcularse únicamente en la dirección dominante, mientras que si h/b≤2 se calculan las 2 direcciones por separado.

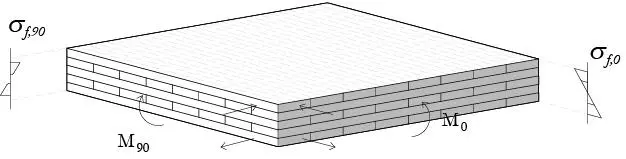
FIGURA 1.4.9 Se asume que la separación de tensiones biaxiales en diferentes láminas permite analizar cada dirección por separado (después de Wallner-Novak et al. 2013).

Flexión esviada

Este tipo de flexión sí produce tensiones en las mismas láminas, por lo que se combina linealmente tal como si fuese en MLE, aunque por el momento no se propone ningún factor de minoración de la combinación por el hecho de que las tensiones pico se produzcan en una región muy reducida (tal como km minora la combinación en MLE), así es que la verificación resultaría

Combinación de cortantes

En determinadas situaciones, como por ejemplo en vigas de CLT solicitadas a flexión en su plano se producen interacciones de tensiones tales como el corte longitudinal (debido al corte transversal aplicado por la carga) más el corte torsional (debido a la tendencia a rotar en torno al adhesivo interlaminar de tablones). Por lo general en la actualidad, se asume que la combinación de cortantes es lineal. Se recomienda consultar la Sección 1.3.12 para más detalles.

1.4.10 Resumen de verificaciones analíticas en miembros de CLT

El resumen de las verificaciones analíticas se presenta en la Tabla 1.4.10. La posible adaptación de la norma NDS con el resumen de factores para conversión de ASD a LRFD se muestra en el Anexo C3.

TABLA 6.4.10 Resumen de verificaciones analíticas en miembros de CLT.
Verificación	Expresión o detalle
Tracción paralela
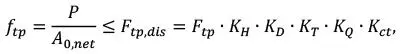en Europa se permite
Tracción perpendicular	Similar a MLE,
Extracción directa solo en cargas bajas, sino transformar a compresión normal y verificar también carga puntual
Compresión paralela
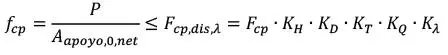con factor por pandeo empleando rigideces efectivas. Si hay apoyo usar ancho efectivo. El pandeo en el plano para paneles estrechos puede ser requerido.
Compresión perpendicular
habiendo especificaciones especiales para Kcn y Aapoyo.
Flexión fuera del plano
y flecha con rigidez aparente o método contrastado, con o sin incrementar el factor de creep.
Flexión en el plano
con precaución de reducción de rigidez torsional en el factor de vuelco lateral torsional. La combinación de corte longitudinal + rodadura se asume lineal pero no está normalizada.
Cortante transversal
recomendando aplicar Kr convencional y refuerzos donde sea necesario y considerando3
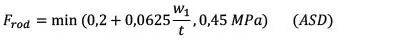Cortante en el plano
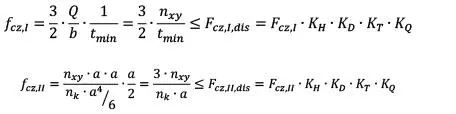Combinación de esfuerzos	Interacción flexión-compresión axial amplificada.Flexión biaxial separada si es que h/b≤2.Flexión esviada con combinación lineal sin reducción.Combinación de corte se asume lineal.
Algunos desarrollos en curso	Determinación de verificaciones para torsión.Afinado de fórmulas de combinación de cortantes.Combinación esfuerzos axiales en elementos compuestos.Adaptación fórmulas para elementos curvos.

1.5 DISEÑO DE UNIONES