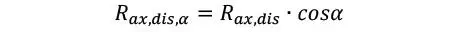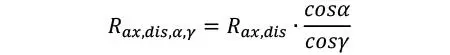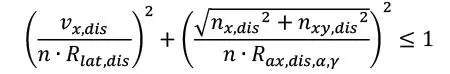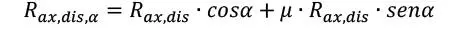Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Otra medida común para mitigar el efecto de los huecos, consiste en insertar los conectores con cierta inclinación, especialmente cuando los conectores se instalan en los boredes del panel. En efecto, es una práctica muy habitual que las líneas de conectores adquieran cierta angulación para evitar solicitaciones puramente axiales. Del Capítulo 1 del libro “Conceptos avanzados del diseño estructural con madera. Parte I” debe recordarse, que, si bien esta práctica puede incrementar en cierto grado la capacidad y de forma muy notable la rigidez, tiende a reducir considerablemente la ductilidad.

En función de la disposición geométrica de los conectores respecto del CLT, podemos distinguir 2 situaciones bien diferentes en cuanto a la influencia de los huecos:

En el caso de conectores dispuestos en las caras del CLT y solicitados lateralmente, las propiedades mecánicas pueden verse no muy afectadas por la presencia de huecos. Igualmente, para conectores en caras del CLT solicitados axialmente, la capacidad podría no verse muy afectada si es que el conector tiene una longitud mínima; por lo general se recomienda que conectores en caras solicitados axialmente atraviesen al menos 3 capas del CLT para minimizar la probabilidad de pérdida de anclaje por huecos, especialmente para conectores de pequeños diámetros.

En el caso de conectores dispuestos en los bordes del CLT y solicitados lateral y axialmente, la capacidad podría verse seriamente perjudicada, especialmente en conectores de pequeño diámetro, si es que coinciden con un hueco o ranura e inserciones axiales en la fibra. Tal como se detalla posteriormente, en estas situaciones principalmente se emplean tornillos autoperforantes dispuestos con cierta angulación respecto de la fibra.

1.5.4 Concepción de desangulaciones 3D y simplificaciones en conectores inclinados

En un contexto en el que los conectores pueden disponerse de forma inclinada en bordes y caras de elementos tipo panel, que además pueden estar sometidos a fuerzas con cualquier angulación, resulta más que conveniente establecer un sistema más completo de definición de inclinaciones y fuerza. En concreto debemos diferenciar claramente 3 angulaciones (ver Figura 1.5.4.1) y 1 disposición:

1 Ángulo de inserción del conector (α, ángulo fibra-conector en el plano del conector).

2 Desangulación fuerza-fibra de la capa más externa del CLT (β, fuerza-fibra externa en el plano perpendicular al plano del conector)

3 Ángulo de la resultante de fuerzas en el plano del conector respecto de la fibra (γ, fuerza-fibra en plano de conector).

4 Conector dispuesto en caras (plano del CLT) o en bordes (grueso del CLT).

Tras esta definición, es evidente que podemos disponer conectores inclinados a una angulación α, sometidos a una fuerza que forma un ángulo β respecto del plano de los conectores, y donde a su vez la fuerza puede presentar cierta desangulación γ con la fibra en el plano de conectores. Asimismo, estos conectores pueden estar dispuestos en las caras o en los bordes, ver Figura 1.5.4.1. Afortunadamente para el diseñador, bajo esta complejidad, es habitual tomar en consideración diversas simplificaciones (ver los fundamentos de dichas simplificaciones de forma más detallada en el Capítulo 1 del libro “Conceptos avanzados del diseño estructural con madera. Parte I”):

Normalmente se asume que la compresión se transfiere por contacto de panel a panel.

La fuerza fuera del plano en donde el conector forma su inclinación, se asume que es absorbida principalmente por la capacidad lateral del conector. La capacidad lateral se calcula de acuerdo a Johansen, pero tomando como longitud la longitud inclinada del tornillo.

Si la fuerza resultante en el plano del tornillo tiene una componente de tracción (separación) respecto del plano de corte, se asume igualmente que ésta es principalmente resistida por su capacidad axial, ya que la rigidez axial es muy superior a la rigidez lateral. La capacidad axial es aquella correspondiente a la mínima capacidad de los modos de falla posibles (similares a los de las uniones convencionales).

FIGURA 1.5.4.1 Estandarización de la complejidad angular en conectores inclinados de CLT. El conector puede estar dispuesto en caras o bordes con una inclinación α. La fuerza a la que está sometido (en el plano de corte en la realidad, en la figura representada sobre la cabeza del tornillo para facilitar la visualización) puede tener una componente perpendicular al plano del tornillo (β), y además tener una componente de tracción en el propio plano del tornillo (γ). Suele asumirse que la capacidad lateral resiste la fuerza perpendicular al plano del tornillo, mientras que la capacidad axial resiste la fuerza (con o sin tracción respecto del plano de corte) en el plano del tornillo.

De esta forma, por ejemplo, para un tornillo con un ángulo α sometido a un corte simple en el plano del tornillo (γ = 0), se asume que la fuerza se resiste principalmente por extracción, así es que la verificación se obtiene por simple equilibrio trigonométrico de fuerzas

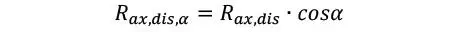
Si además de lo anterior, existe una fuerza de separación respecto del plano de corte (γ ≠ 0), podemos estimar análogamente la capacidad como

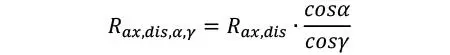
Por otra parte, la componente β se verificaría directamente por la capacidad al corte lateral del tornillo. Afortunadamente, tal como se mostrará en apartados sucesivos, la desangulación β no es tan importante en el CLT como en el resto de productos de madera. En el caso general de un tornillo inclinado con una fuerza desangulada (es decir α, β, γ ≠ 0), la verificación se simplificaría a

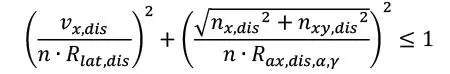
donde en la fórmula anterior, vx se refiere a la solicitación de corte fuera del plano por metro de ancho, nx se refiere a la solicitación vertical de levantamiento, y nxy se refiere al corte en el plano de los tornillos, ver Figura 1.5.3.2 para una ilustración de la típica configuración de tornillos y fuerzas en elementos estructurales convencionales.

FIGURA 1.5.3.2 Típica simplificación en la verificación de líneas de tornillos inclinadas solicitadas a cargas desanguladas en el CLT. Se asume que la totalidad de la carga fuera del plano de los tornillos, vx debe ser resistida por la capacidad lateral, mientras que las fuerzas axiales de extracción nxy el corte en el plano nxy deben ser resistidos enteramente por la capacidad axial desangulada de los mismos (basado en Ringhofer 2010).

En caso particular de que la resultante de la fuerza en el plano de los tornillos no tenga ninguna componente de tracción (γ ≥ 90), y el corte esté efectivamente generando una tracción del tornillo, algunos autores sugieren incluir el efecto cuerda (en caso de haberlo) en el cálculo de la capacidad oblicua tal que

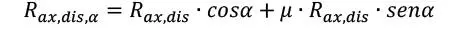
lo que tiene que ser capaz de resistir la acción de corte en el plano

No obstante, es importante notar que la consideración del efecto cuerda tan sólo se lleva a cabo en uniones en las que en estado deformado esté asgurado que no habrá levantamiento. Típicamente esto sucede en las uniones muro-techo, si es que la succión de viento no es elevada, pero no en las uniones muro-losa muro (estas sufren momento por vuelco). En apartados sucesivos se aclararán más aspectos en relación a la verificación de líneas de unión.