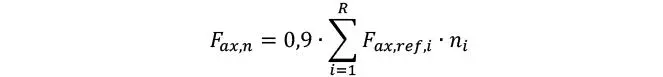Finalmente, en el caso de tornillos en cruz dispuestos a 45°, la capacidad lateral, necesaria para resistir la fuerza fuera del plano de los tornillos se asume como el doble de la capacidad de un solo tornillo
Por otro lado, en el plano de la cruz conformada por los tornillos, se asume que la resistencia para soportar la tracción pura de la cruz (γ = 0) es similar a la resistencia para resistir el corte puro en el plano (γ ≥ 90) e igual a la resultante de resistencia axial obtenida por el teorema de Pitágoras, considerando la resistencia axial de un único tornillo; es decir
De modo que en este caso la verificación
En la Sección 1.6.3 se ejemplifican todas estas verificaciones para las típicas uniones encontradas en un edificio de CLT.
1.5.5 Efecto refuerzo de lámina perpendicular e incremento de ductilidad local en conectores laterales insertados en caras
Una característica muy positiva del CLT frente a la MLE, madera maciza y otros productos es que, más allá de que la ductilidad global sea inferior por disminuir significativamente la redundancia de las uniones y elementos estructurales, la ductilidad local aportada por un solo conector lateral insertado en las caras del CLT es por lo general superior, especialmente en conectores gruesos y asociados a modos de falla frágiles. Esto se debe a que las capas transversales actúan como un refuerzo generando un efecto de refuerzo por lámina perpendicular y evitando modos de falla frágiles. Recuérdese que para la mayoría de conectores (a excepción de clavos delgados y conectores similares); la desangulación carga-fibra tiene una influencia notable en la resistencia al aplastamiento y la posibilidad de fallo frágil (individual o en grupo), por lo tanto, la posibilidad de fallo frágil puede minimizarse si es que existe una capa transversal, lo que se traduce en varios casos en un incremento notable de la ductilidad local, ver Figura 1.5.5.
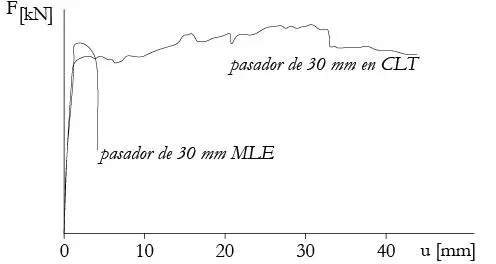
FIGURA 1.5.5 Incremento de ductilidad local de un pasador de 30 mm, por efecto del refuerzo transversal de las capas de CLT (basado en Schickhofer et al. 2009).
Este efecto, se considera habitualmente en el cálculo según ELU, para conectores insertados en las caras y solicitados lateralmente mediante la no disminución del número efectivo de conectores si es que se respetan los espaciamientos (nef=n), lo que análogamente resultaría en un factor hilera Ku=1 según ASD. Esta regla no aplica en conectores insertados en los bordes del CLT, pues en esa situación no existe el efecto de refuerzo por capas ortogonales a lo largo de la longitud del conector.
1.5.6 Posibilidad de fallo por tracción perpendicular de conectores laterales en bordes solicitados fuera del plano
Los conectores situados en los bordes pueden estar cargados por una fuerza lateral que es paralela al plano del CLT, o bien perpendicular al mismo. En este último caso, existe la posibilidad de fallo frágil por tracción perpendicular, lo que puede disminuir bastante la capacidad de la unión. Por el momento esto se controla principalmente empleando un mínimo espesor de láminas del CLT. No obstante, diversos autores recomiendan evitar esta disposición para determinados conectores.
1.5.7 Recomendaciones generales sobre el uso de conectores en el CLT según su disposición y el tipo de carga
En vista a los aspectos mencionados anteriormente, las recomendaciones generales respecto del uso de conectores en el CLT se muestran en la Tabla 1.5.7.
| TABLA 1.5.7 Recomendaciones del uso de conectores respecto su disposición en el CLT y el tipo de carga (basado en Schickhofer et al. 2009). |
|
En caras del CLT, recomendado para |
En los bordes del CLT, recomendado para |
|
Flat |
Fax |
Flat |
Fax |
| Clavos corrugados |
✓ |
✓ |
✕ |
✕ |
| Pasadores y pernos |
✓ |
✕ |
✕ |
✕ |
| Tornillos autoperforantes |
✓ |
✓ |
✓ |
✓ |
1.5.8 Procedimiento de diseño
En términos generales, el procedimiento para diseñar uniones en CLT es el mismo que en las uniones mecánicas convencionales. Pese a que algunos autores han propuesto ecuaciones específicas que permiten afinar la descripción del comportamiento de las uniones, programas experimentales tremendamente exhaustivos desarrollados en Europa han validado la aplicación de las ecuaciones de Johansen para CLT-CLT y CLT-metal en simple y doble cortadura. Además, y con la salvedad de lo expuesto posteriormente, los modos de falla de extracción axial y oblicua son los mismos que para el resto de productos de madera. Principalmente, son 2 las diferencias al diseñar uniones de CLT respecto de uniones convencionales:
1 La capacidad de extracción axial y aplastamiento lateral difieren —en diferente magnitud según disposición del conector y dirección de la carga— respecto de los valores de madera maciza, MLE y LVL. Por lo anterior, por lo general se requiere la aplicación de ecuaciones específicas para calcular dichas capacidades, lo que se detalla en los apartados sucesivos.
2 Una vez determinadas las capacidades de aplastamiento y extracción axial con las ecuaciones específicas del CLT, las predicciones de Johansen para carga lateral, los modos de falla axiales, y las combinaciones correspondientes para uniones oblicuas resumidas anteriormente, son aplicables en el CLT, pudiendo predecir la capacidad con precisión y conservadurismo. No obstante, la ocurrencia de modos de falla en grupo son diferentes, en especial bajo la acción de cargas de extracción axial, por lo que se requieren diferentes espaciamientos para permitir la redistribución de tensiones. Los espaciamientos necesarios y otros detalles geométricos se detallan en la Tabla 1.5.8 e ilustran en la Figura 1.5.8. Finalmente, la consideración del efecto hilera (nef en EC5, Ku en NCh1198) difiere sensiblemente de la determinación en madera maciza o MLE:
1 Para conectores dispuestos en caras, y solicitados lateralmente n=nef (Ku=1) por el efecto del refuerzo de las capas perpendiculares del CLT.
2 Para conectores dispuestos en los bordes y solicitados lateralmente, no existe efecto refuerzo perpendicular y se recomienda calcular nef y Ku de acuerdo a las especificaciones para madera maciza y MLE.
3 Para grupos de conectores dispuestos en caras o bordes y solicitados axialmente, se observa frecuentemente fallo en grupo por tracción perpendicular y corte, por lo que se recomienda minorar la capacidad del conjunto según la siguiente ecuación
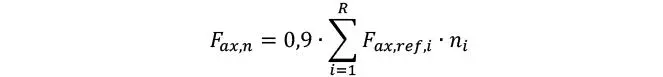
donde R es el número de configuraciones en lo relativo al ángulo de inserción tornillo-fibra (α), Fax,ref,i es la capacidad a la extracción calculada para cada conector individual y ni es el número de conectores que existen para cada configuración de ángulo α.
| TABLA 1.5.8 Espaciamientos y restricciones geométricas en uniones de CLT. |
| Espaciamientos básicos según disposición en cara o borde y tipo de conector (ver geometría en Figura 1.5.8) |
| Conector |
Disposición |
a1 |
a2 |
a3,t |
a3,c |
a4,t |
a4,c |
| Tornillos autoperforantes |
Caras |
4 d |
2.5 d |
6 d |
6 d |
6 d |
2.5 d |
| Bordes |
10 d |
3 d |
12 d |
7 d |
- |
5 d |
| Clavos corrugados |
Caras |
(3+3 cos β) d |
3 d |
(7+3 cos β) d |
6 d |
(3+4 sin β) d |
3 d |
| Pasadores |
Caras |
(3+2 cosβ) d |
3 d |
5 d |
4 d sinβ (min 3 d) |
3 d |
3 d |
| Bordes |
4 d |
3 d |
5 d |
3 d |
- |
3 d |
| Ajuste de espaciamiento longitudinal y transversal según ángulo fibra-conector (α) |
|
| * 5 d si se inserta en la misma lámina, 2.5 d si se inserta en láminas diferentes |
| Restricciones geométricas en cuanto a espesor mínimo de panel, laminaciones y conectores |
| ConectortCLT, mintℓaminación,minℓpenetrac.min*Tornillos autoperforantes10 dd ≤ 8 mm: 2 d10 dd > 8 mm: 3 dPasadores6 dd5 d |
| Espaciamiento máximo según tipo de conector |
| Tipo de uniónemax (mm)CLT - CLT con tornillos500CLT - MLE con tornillos500CLT - Acero con tornillos750CLT - hormigón o acero con ángulos de corte1,000 |
FIGURA 1.5.8 Geometría de espaciamientos para conectores dispuestos en caras (arriba) y en bordes (abajo) según recomendaciones europeas.
Читать дальше