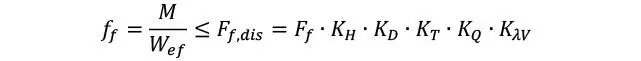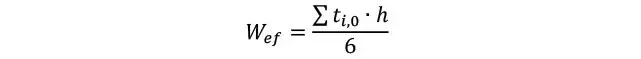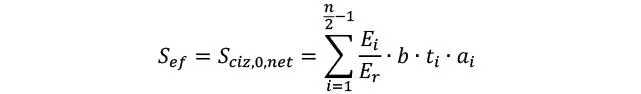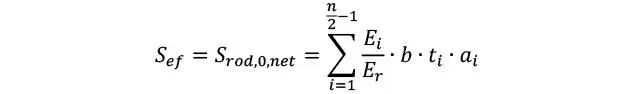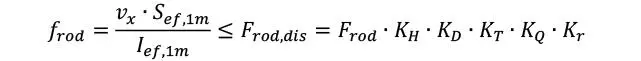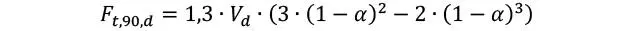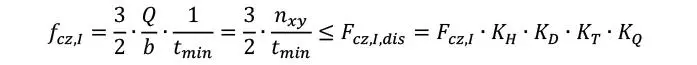Pablo Guindos - Conceptos avanzados del diseño estructural con madera

Los factores de creep que se están proponiendo para el CLT son en esencia similares a la MLE, y en algunos casos similares también al terciado. En vista del estado del arte internacional, se sugiere emplear los mismos valores que la madera o bien incrementar estos valores un 10%, debido a que por lo general el efecto del creep es bastante mayor en piezas solicitadas a cortante de rodadura.

1.4.6 Flexión en el plano

Especialmente en Europa, algunos autores han estado proponiendo el uso de vigas de CLT para flectar en su propio plano, especialmente en consideración del efecto de “refuerzo” que las láminas perpendiculares tienen frente a la ocurrencia típica de tensiones perpendiculares propias de vigas curvas o/y canto variable. También es posible encontrar paneles de CLT que, debido a sus condiciones de carga y apoyo, estén sometidos a flexiones en el plano. Dichas aplicaciones requieren todavía cierta investigación, pero por el momento se sugiere aplicar un criterio de verificación similar a la flexión fuera del plano tal que

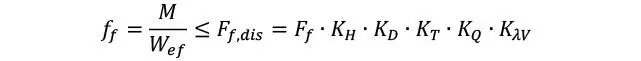
Donde únicamente las láminas paralelas contribuyen efectivamente, ver Figura 1.4.6.

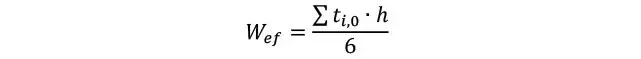
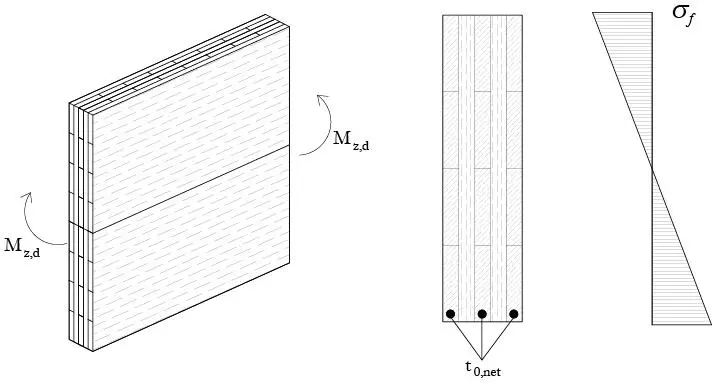
FIGURA 1.4.6 En la aplicación del CLT como elementos tipo viga para flectar en el plano, únicamente las láminas paralelas contribuyen; sin embargo, se tiene la ventaja de reforzar la dirección perpendicular a la fibra, lo que puede ser importante en diversas situaciones tales como vigas curvas o/y canto variable (después de Wallner-Novak et al. 2013).

Nótese que en este caso la aplicación del factor de inestabilidad por vuelco lateral-torsional sí es mucho más probable. La determinación de este factor de acuerdo a la NDS, es completamente similar al de elementos tipo viga; sin embargo, es importante que el lector tenga en cuenta ciertos parámetros durante esta verificación. En concreto, es importante mencionar que, para la derivación de la tensión crítica de vuelco lateral-torsional, sencillamente se considera (implícitamente en la verificación analítica de las normativas) la rigidez torsional de la sección transversal (GTIT). Tal como se introdujo en la Sección 1.2.1 (momento de inercia torsional de la sección transversal) y Sección 1.3.9, tanto el momento de inercia torsional como el módulo de rigidez torsional son inferiores a los valores esperados en vigas rectangulares equivalentes. Por lo anterior, la verificación debe realizarse con cautela mientras no se afine en la prescripción de las ecuaciones correspondientes. Por otra parte, Wallner-Novak et al. 2013, sugieren ecuaciones aproximativas que permiten estimar el momento torsor necesario para restringir lateralmente una viga de CLT en sus extremos, como una determinada fracción del momento máximo de la viga, Mmax

En el caso de restringir puntualmente el vuelco lateral torsional de un panel de CLT con n puntales espaciados regularmente en el borde flexo-comprimido de una viga de altura h y longitud l, la fuerza axial uniforme que debe ser empleada de forma adicional a la fuerza horizontal correspondiente (p.ej. por viento) de los puntales puede estimarse aproximadamente como

La ecuación anterior no es especial para el CLT, sino que se deriva de las típicas ecuaciones de dimensionado de elementos de arriostramiento de madera (ver detalles en el Capítulo 5 del libro “Conceptos avanzados del diseño estructural con madera. Parte I”.

Respecto de la resistencia a flexión en el plano, cabe mencionar que, si bien la normativa norteamericana permite emplear el mismo valor resistente que una viga normal, en Europa por seguridad se propone reducir la resistencia en un 15% para esta verificación, mientras no se tengan más datos experimentales.

1.4.7 Cortante perpendicular a la placa

De forma similar a la flexión, tanto la normativa norteamericana como el método europeo proponen un método simplificado. La solicitación cortante se calcula como de costumbre con la inercia y el momento estático efectivos

donde recordemos que

Y el momento estático efectivo se refiere al correspondiente para el cizalle

O si se da el caso de que la lámina intermedia no fuese longitudinal

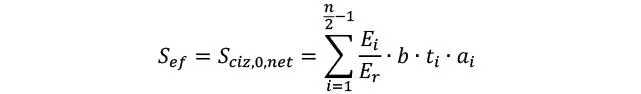
En el caso de calcular con el cortante transversal correspondiente a una tira de 1 metro de ancho

Además del cizalle, debe de verificarse el posible fallo de rodadura en las láminas transversales al eje de la flexión, de modo que la verificación resulta

donde en este caso

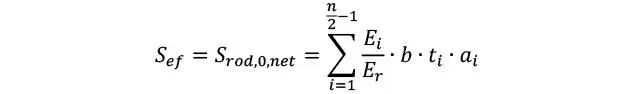
o por supuesto

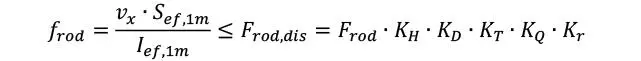
Lo más habitual es que domine la rodadura, por lo que en muchos textos aparece únicamente la verificación por rodadura. Véase una discusión detallada de los valores resistentes del cortante de rodadura según ASD y ELU en la sección 6.1.3.

Con respecto al factor de reducción por rebaje, Kr, actualmente la normativa norteamericana propone emplear el mismo factor que para vigas, y lo mismo sucede en Europa mientras no haya más evidencias de un diferente comportamiento. En caso de que el cortante no verifique al emplear Kr (aunque sí sin considerar ese factor), debe aplicarse un refuerzo tal como se indica en el libro “Conceptos avanzados del diseño estructural con madera. Parte I”, Capítulo 2, Sección 2.1.3, donde la fuerza de tracción que debe resistir el refuerzo es una fracción del corte de diseño y se repite aquí por conveniencia:

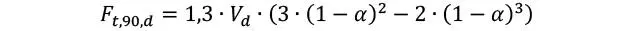
1.4.8 Cortante en el plano

Tal como se detalló en la sección 1.3.7. suceden de forma simultánea 2 mecanismos de falla que deben ser verificados: el cortante transversal de los tablones y la torsión en torno al encolado entre láminas. Es importante notar que las verificaciones de ambos fenómenos, se encuentran mayormente en discusión, por lo que diversas fórmulas son propuestas a la fecha. Con respecto a la verificación del mecanismo I (corte transversal de las láminas) se recomienda aplicar

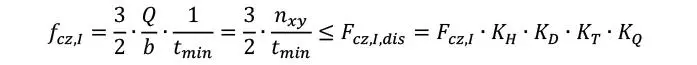
Donde tmin es el valor mínimo entre la suma de espesores de láminas orientadas en dirección vertical, y suma de espesores de láminas orientadas en dirección horizontal, i.e. espesor total de madera que resiste el corte transversal.

Con respecto a la solicitación de corte debida al momento torsor (mecanismo II), esta puede ser determinada como la relación entre el momento torsor, el radio respecto del centro de torsión y el momento polar de inercia, lo que para el caso de en que los tablones tengan el mismo ancho (a), resulta (ver valores para el caso de que los tablones no tengan el mismo ancho en la Sección 1.2.1.):