Anil K. Chopra - Earthquake Engineering for Concrete Dams

(2.6.3)

where

(2.6.4)

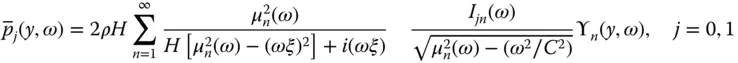
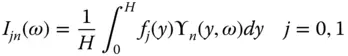
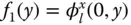in which f 0( y ) = 1 and . For convenience later in defining the added hydrodynamic mass, the preceding pressure functions are defined for the positive x ‐direction upstream, thus giving algebraic signs opposite those of the corresponding equations in Section 2.3, where the positive x ‐direction was downstream.

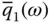Including dam–water interaction, the frequency response function for the modal coordinate associated with the fundamental vibration mode of the dam, Eq. (2.6.1), is a complicated function of excitation frequency ω that contains frequency‐dependent hydrodynamic terms. To develop a simplified analytical procedure, the dam–water system will be modeled by an equivalent SDF system with frequency‐independent values for the hydrodynamic terms. Such a procedure, developed by Chopra (1978) for dam–water systems with non‐absorptive reservoir bottom and later extended to include reservoir bottom absorption (Fenves and Chopra 1985c), is presented next.

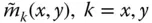The properties of the equivalent SDF system are defined as those of the dam with an empty reservoir modified by an added mass and an added damping that represent the hydrodynamic effects of the impounded water. The mass density , of the equivalent SDF system is defined as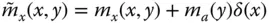

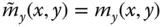
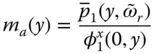
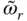(2.6.5a)

(2.6.5b)

where δ ( x ) is the Dirac delta function. Because the hydrodynamic pressure on a vertical upstream face acts in the horizontal direction, the “added mass” m a( y ) applies only to the horizontal displacement of the dam and is concentrated at the upstream face of the dam. The frequency‐independent “added mass” is defined as

(2.6.6)

where the natural vibration frequency of the equivalent SDF system approximates the fundamental resonant frequency of the dam–water system. If the reservoir bottom is absorptive, m a( y ) is complex valued. Thus, it is not a mass quantity in the usual sense; only its real‐valued component contributes to an added mass, whereas the imaginary‐valued component implies an added damping. Furthermore, this added mass representing hydrodynamic effects on a flexible dam differs from the one in Eq. (2.3.25), which was determined assuming the dam to be rigid. It is inappropriate to use the latter in dynamic analysis of dams because they are flexible structures.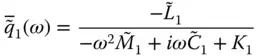

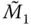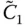The complex‐valued frequency response function for the modal coordinate of the equivalent SDF system will be of the same form as Eq. (2.2.7), but L 1, M 1, and C 1will be different; thus

(2.6.7)

wherein the superscript l = x has been dropped for notational simplicity, and the over‐tilde is included to indicate that the equivalent SDF system models the dam response including dam–water interaction; , , and 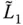are obtained by substituting Eq. (2.6.5)in the standard definitions of generalized mass, damping, and force (Chopra 2017, Chapter 17):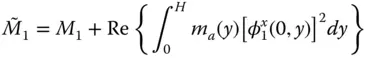

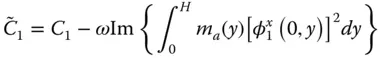
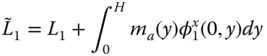
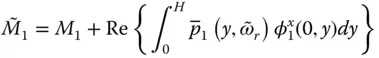
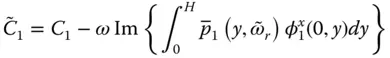
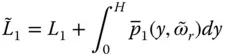
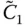(2.6.8a)

(2.6.8b)

(2.6.8c)

and M 1, C 1, and L 1for the dam alone were defined in Section 2.2.1. Substituting Eq. (2.6.6)into Eq. (2.6.8)leads to

(2.6.9a)

(2.6.9b)

(2.6.9c)

We will demonstrate that if the excitation frequency ω that appears in is replaced by the resonant frequency 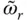, Eq. (2.6.7)will give the same resonant response as the rigorous Eq. (2.6.1). Using the solutions for p 0( y , ω ) and p 1( y , ω ) in Eq. (2.6.3), replacing ω by 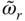in C 1, and recalling Eq. (2.6.2)for the definition of B 0( ω ) and B 1( ω ), Eq. (2.6.9)becomes

(2.6.10a)

(2.6.10b)