The response of the dam is greatly influenced by the frequency ratio, Ω r. i.e. the relative frequencies of the two interacting systems, as demonstrated by Figures 2.5.1and 2.5.3. The percentage decrease in the fundamental resonant frequency of the dam due to dam–water interaction is larger for the smaller values of Ω r, i.e. larger values of E s. The response value at resonance as well as the shape of the response curve in the neighborhood of the natural frequencies of the dam and of the impounded water also depend significantly on the frequency ratio Ω r.
With increasing Ω r, or decreasing E s, the effects of water compressibility on response become smaller and the response curve approaches the result for incompressible water. For systems with Ω r= 2.0, the effects of water compressibility are insignificant in the response to horizontal ground motion ( Figures 2.5.5and 2.5.7) but are still noticeable in the response to vertical ground motion ( Figures 2.5.6and 2.5.8). These results confirm the earlier conclusion that the effects of water compressibility become insignificant for systems with Ω r> 2 or 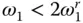 (Chopra 1968), which for the system considered implies E s< 0.63 million psi. However, E sfor mass concrete is generally in the range of 2–5 million psi. Consequently, errors in response results will be significant if water compressibility is ignored. This conclusion will be reinforced further in the context of response to earthquake excitation ( Chapter 6).
(Chopra 1968), which for the system considered implies E s< 0.63 million psi. However, E sfor mass concrete is generally in the range of 2–5 million psi. Consequently, errors in response results will be significant if water compressibility is ignored. This conclusion will be reinforced further in the context of response to earthquake excitation ( Chapter 6).
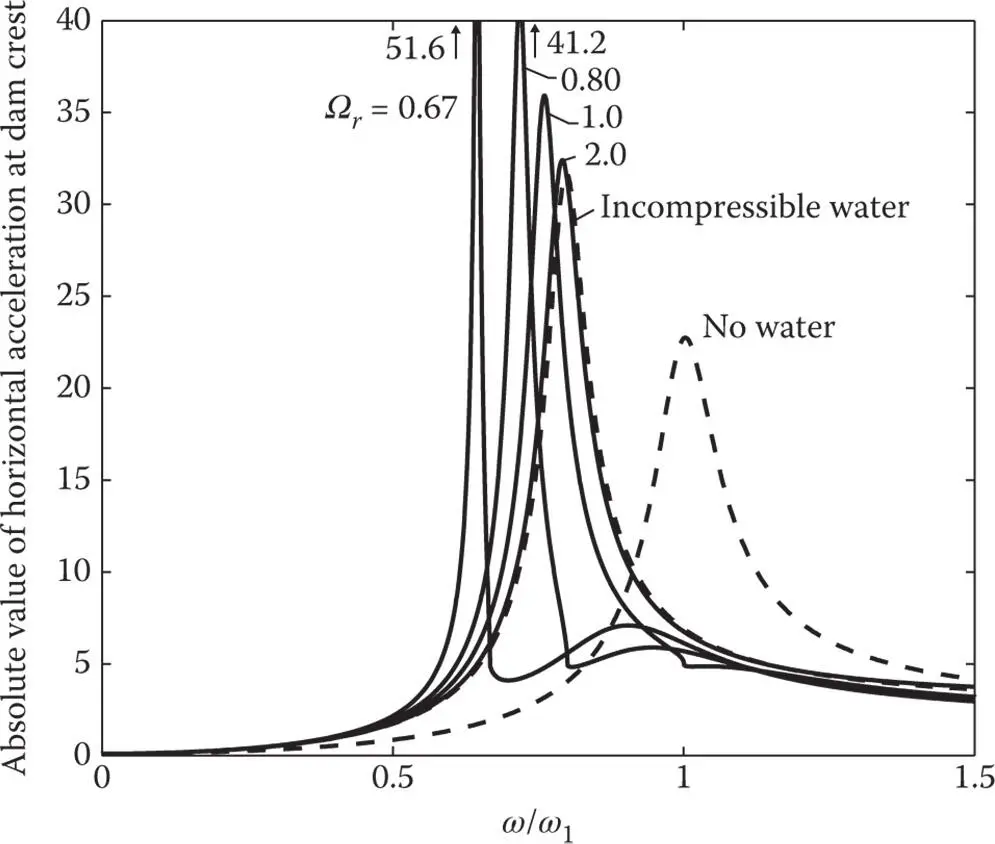
Figure 2.5.5Influence of frequency ratio, Ω r, on dam response to harmonic horizontal ground motion. Results are presented (1) including water compressibility with α = 1 for Ω r= 0.67, 0.80, 1.0, and 2.0 ( E s= 5.67, 3.94, 2.52, and 0.63 million psi); and (2) assuming water to be incompressible.
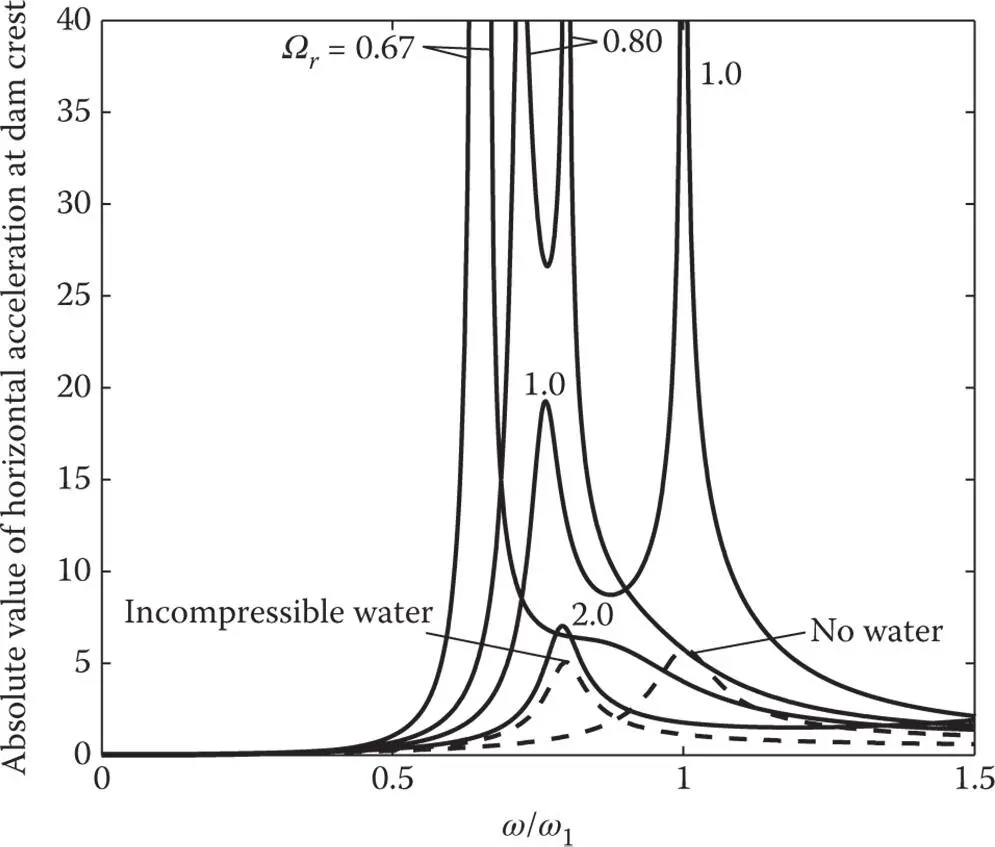
Figure 2.5.6Influence of frequency ratio, Ω r, on dam response to harmonic vertical ground motion. Results are presented (1) including water compressibility with α = 1 for Ω r= 0.67, 0.80, 1.0, and 2.0 ( E s= 5.67, 3.94, 2.52, and 0.63 million psi); and (2) assuming water to be incompressible.
Figure 2.5.7Influence of frequency ratio, Ω r, on dam response to harmonic horizontal ground motion. Results are presented (1) including water compressibility with α = 0.75 for Ω r= 0.67, 0.80, 1.0, and 2.0 ( E s= 5.67, 3.94, 2.52, and 0.63 million psi); and (2) assuming water to be incompressible.
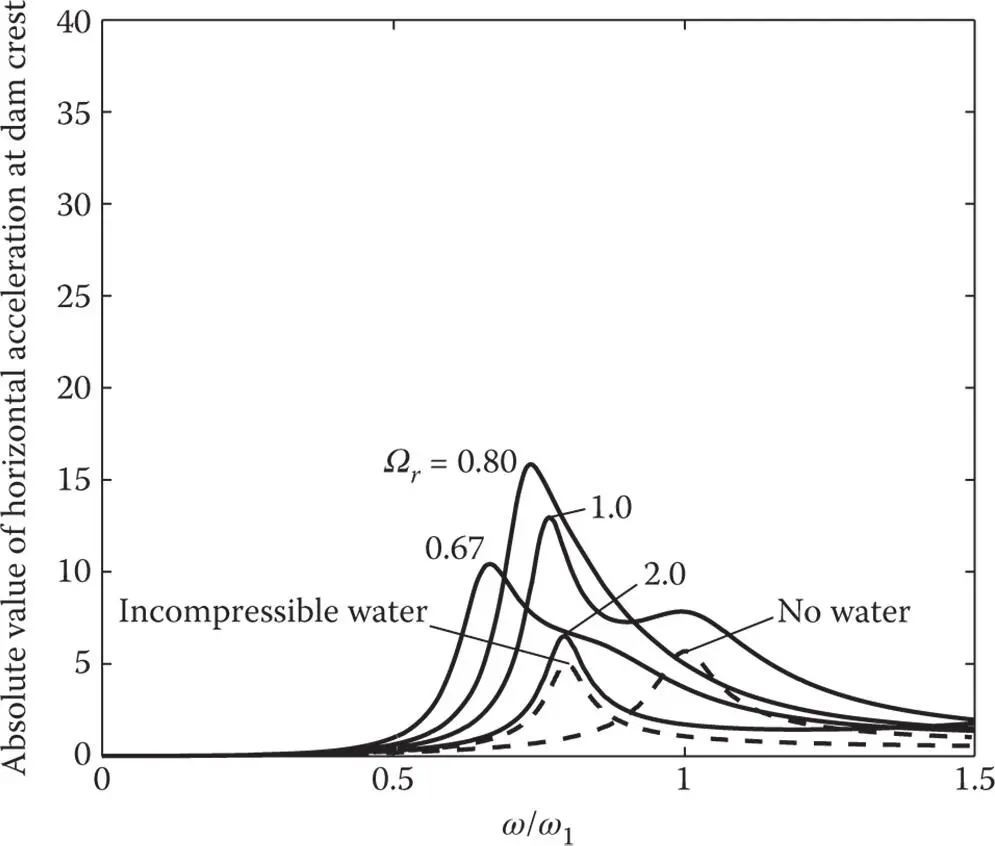
Figure 2.5.8Influence of frequency ratio, Ω r, on dam response to harmonic vertical ground motion. Results are presented (1) including water compressibility with α = 0.75 for Ω r= 0.67, 0.80, 1.0, and 2.0 ( E s= 5.67, 3.94, 2.52, and 0.63 million psi); and (2) assuming water to be incompressible.
2.5.5 Comparison of Responses to Horizontal and Vertical Ground Motions
Comparing the response of the dam to horizontal and vertical ground motions ( Figures 2.5.5and 2.5.6) it is apparent – consistent with common view – that without impounded water the response to vertical ground motion is relatively small because the excitation term 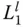 in Eq. (2.4.10)is much smaller for vertical ground motion ( l = y ) than for horizontal ground motion ( l = x ). With impounded water in the reservoir, the response is affected by the added hydrodynamic mass, damping, and force terms in Eq. (2.4.10). Because the added hydrodynamic mass and damping are independent of the excitation direction, the response functions due to horizontal and vertical ground motions display the same resonant frequency and effective damping. However, the added force is associated with hydrodynamic pressures acting in the horizontal direction on the vertical upstream face of a rigid dam, whether the ground motion is horizontal or vertical. In the latter case,
in Eq. (2.4.10)is much smaller for vertical ground motion ( l = y ) than for horizontal ground motion ( l = x ). With impounded water in the reservoir, the response is affected by the added hydrodynamic mass, damping, and force terms in Eq. (2.4.10). Because the added hydrodynamic mass and damping are independent of the excitation direction, the response functions due to horizontal and vertical ground motions display the same resonant frequency and effective damping. However, the added force is associated with hydrodynamic pressures acting in the horizontal direction on the vertical upstream face of a rigid dam, whether the ground motion is horizontal or vertical. In the latter case, 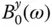 is much larger than the small
is much larger than the small 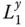 . As a result, hydrodynamic effects (including water compressibility) cause a larger increase in response to vertical ground motion than in response to horizontal ground motion. This is apparent by comparing the response curves for the dam without water and with water associated with the two excitations ( Figures 2.5.1versus 2.5.2and Figures 2.5.3versus 2.5.4).
. As a result, hydrodynamic effects (including water compressibility) cause a larger increase in response to vertical ground motion than in response to horizontal ground motion. This is apparent by comparing the response curves for the dam without water and with water associated with the two excitations ( Figures 2.5.1versus 2.5.2and Figures 2.5.3versus 2.5.4).
Putting this issue in historical context, the response of concrete gravity dams to the vertical component of ground motion was overestimated in the earliest studies based on the assumption of non‐absorptive reservoir bottom (Chopra and Chakarabarti 1973, 1974). An absorptive reservoir bottom gives a more plausible estimate of the response to vertical ground motion and its smaller contribution to the total earthquake response of the dam (Fenves and Chopra 1983). Although not negligible, this contribution is of secondary importance. Thus, the response to only the horizontal component of ground motion is considered in developing the procedure for simplified analysis of two‐dimensional dam–water–foundation systems ( Sections 2.6, 3.4, and 3.5); this procedure is intended for preliminary analysis and design of dams.
2.6 EQUIVALENT SDF SYSTEM: HORIZONTAL GROUND MOTION
It was shown in Section 2.4that including the interaction between the dam and compressible water results in the following complex‐valued frequency response function for the modal coordinate due to horizontal ground motion ( Eq. (2.4.10)with the superscript l = x dropped):
(2.6.1) 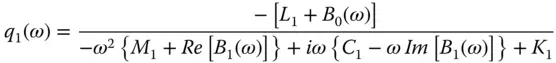
in which the hydrodynamic terms B 0( ω ) and B 1( ω ) are equivalent to those in Eq. (2.4.10)but are now defined slightly differently:
(2.6.2a) 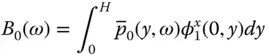
(2.6.2b) 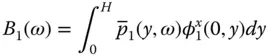
where  and
and 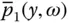 are frequency response functions for the hydrodynamic pressure on the upstream face due to horizontal ground acceleration of a rigid dam, and acceleration of a dam in its fundamental mode of vibration, respectively:
are frequency response functions for the hydrodynamic pressure on the upstream face due to horizontal ground acceleration of a rigid dam, and acceleration of a dam in its fundamental mode of vibration, respectively:
Читать дальше

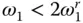 (Chopra 1968), which for the system considered implies E s< 0.63 million psi. However, E sfor mass concrete is generally in the range of 2–5 million psi. Consequently, errors in response results will be significant if water compressibility is ignored. This conclusion will be reinforced further in the context of response to earthquake excitation ( Chapter 6).
(Chopra 1968), which for the system considered implies E s< 0.63 million psi. However, E sfor mass concrete is generally in the range of 2–5 million psi. Consequently, errors in response results will be significant if water compressibility is ignored. This conclusion will be reinforced further in the context of response to earthquake excitation ( Chapter 6).



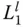 in Eq. (2.4.10)is much smaller for vertical ground motion ( l = y ) than for horizontal ground motion ( l = x ). With impounded water in the reservoir, the response is affected by the added hydrodynamic mass, damping, and force terms in Eq. (2.4.10). Because the added hydrodynamic mass and damping are independent of the excitation direction, the response functions due to horizontal and vertical ground motions display the same resonant frequency and effective damping. However, the added force is associated with hydrodynamic pressures acting in the horizontal direction on the vertical upstream face of a rigid dam, whether the ground motion is horizontal or vertical. In the latter case,
in Eq. (2.4.10)is much smaller for vertical ground motion ( l = y ) than for horizontal ground motion ( l = x ). With impounded water in the reservoir, the response is affected by the added hydrodynamic mass, damping, and force terms in Eq. (2.4.10). Because the added hydrodynamic mass and damping are independent of the excitation direction, the response functions due to horizontal and vertical ground motions display the same resonant frequency and effective damping. However, the added force is associated with hydrodynamic pressures acting in the horizontal direction on the vertical upstream face of a rigid dam, whether the ground motion is horizontal or vertical. In the latter case, 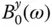 is much larger than the small
is much larger than the small 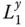 . As a result, hydrodynamic effects (including water compressibility) cause a larger increase in response to vertical ground motion than in response to horizontal ground motion. This is apparent by comparing the response curves for the dam without water and with water associated with the two excitations ( Figures 2.5.1versus 2.5.2and Figures 2.5.3versus 2.5.4).
. As a result, hydrodynamic effects (including water compressibility) cause a larger increase in response to vertical ground motion than in response to horizontal ground motion. This is apparent by comparing the response curves for the dam without water and with water associated with the two excitations ( Figures 2.5.1versus 2.5.2and Figures 2.5.3versus 2.5.4).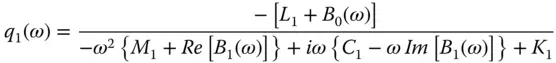
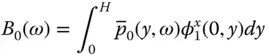
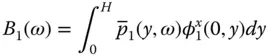
 and
and 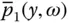 are frequency response functions for the hydrodynamic pressure on the upstream face due to horizontal ground acceleration of a rigid dam, and acceleration of a dam in its fundamental mode of vibration, respectively:
are frequency response functions for the hydrodynamic pressure on the upstream face due to horizontal ground acceleration of a rigid dam, and acceleration of a dam in its fundamental mode of vibration, respectively:










