The complex‐valued frequency response function, 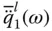 , is a dimensionless response factor representing the ratio of horizontal acceleration at the dam crest to unit free‐field ground acceleration in the l (= x or y ) direction. For each case mentioned above, the absolute value of this complex‐valued response factor is plotted against the normalized excitation frequency ω / ω 1. When presented in this form, the results apply to dams of all heights with the idealized triangular cross section, and chosen Ω r, H / H s, and α values.
, is a dimensionless response factor representing the ratio of horizontal acceleration at the dam crest to unit free‐field ground acceleration in the l (= x or y ) direction. For each case mentioned above, the absolute value of this complex‐valued response factor is plotted against the normalized excitation frequency ω / ω 1. When presented in this form, the results apply to dams of all heights with the idealized triangular cross section, and chosen Ω r, H / H s, and α values.
2.5.3 Dam–Water Interaction Effects
Frequency response functions for dams subjected to horizontal and vertical ground motions are presented in Figures 2.5.1– 2.5.4for two selected values of Ω r= 0.67 and 1.0. Each plot contains response curves for the dam with full reservoir for five values of α and the response curve for the dam alone, i.e. with an empty reservoir. The latter is the familiar response curve for a SDF system with frequency‐independent mass, stiffness, and damping parameters. However, dam–water interaction including water compressibility introduces frequency‐dependent terms in Eq. (2.4.10), resulting in complicated shapes for the response curves.
The frequency response function due to horizontal ground motion displays strongly resonant behavior with large amplification over an especially narrow frequency band because of dam–water interaction and water compressibility. The single resonant peak in the response of the dam without water may become two resonant peaks for a full reservoir if the reservoir bottom is non‐absorptive, a behavior that develops for systems with smaller Ω ror stiffer dams ( Figure 2.5.1). With increasing wave absorption at the reservoir bottom, i.e. decreasing α , the first resonant peak is reduced, whereas the second peak is increased, and for a small enough α the two peaks coalesce, resulting in a single resonant peak at an intermediate resonant frequency. For systems with the larger Ω rvalue, or relatively flexible dams, only a single resonant peak develops for all values of α ( Figure 2.5.3). For such systems, as α decreases, increased absorption of energy through the reservoir bottom further reduces the resonant amplitude, with little change in the resonant frequency. The fundamental resonant frequency of the dam including hydrodynamic effects is lower than both the natural frequency ω 1of the dam alone and the fundamental natural frequency 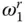 of the impounded water.
of the impounded water.
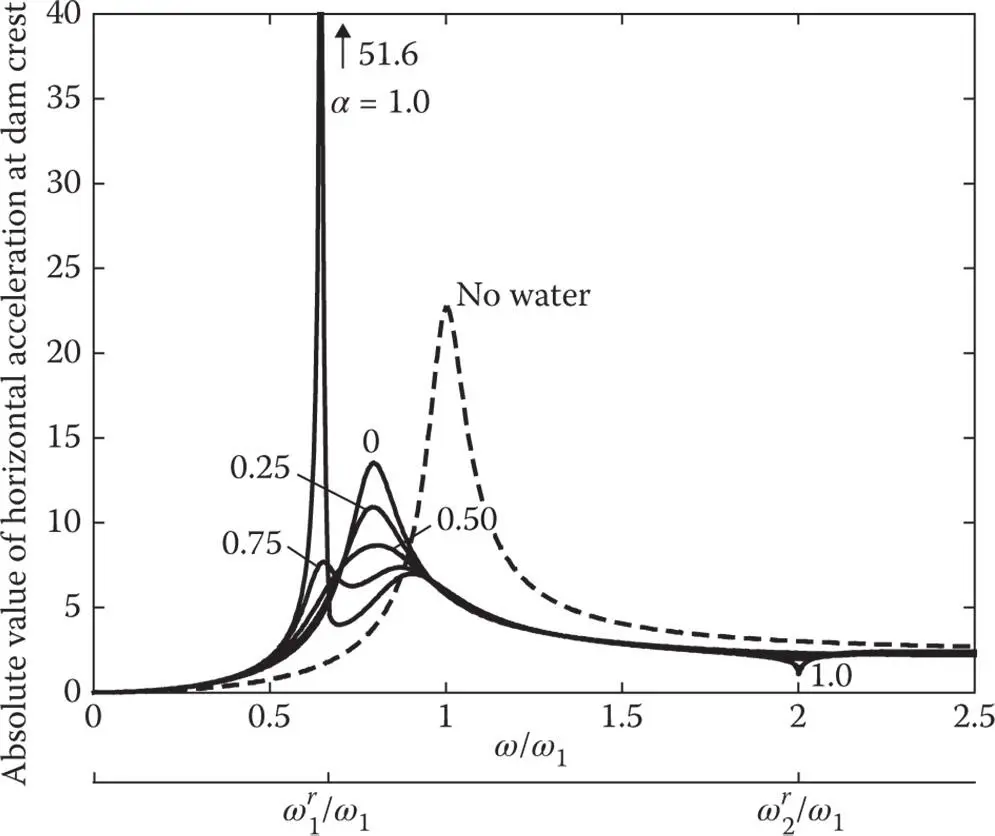
Figure 2.5.1Dam response to harmonic horizontal ground motion; frequency ratio, Ω r= 0.67, i.e. E s= 5.67 million psi; α = 1.0, 0.75, 0.50, 0.25, and 0; response of dam alone is also shown.
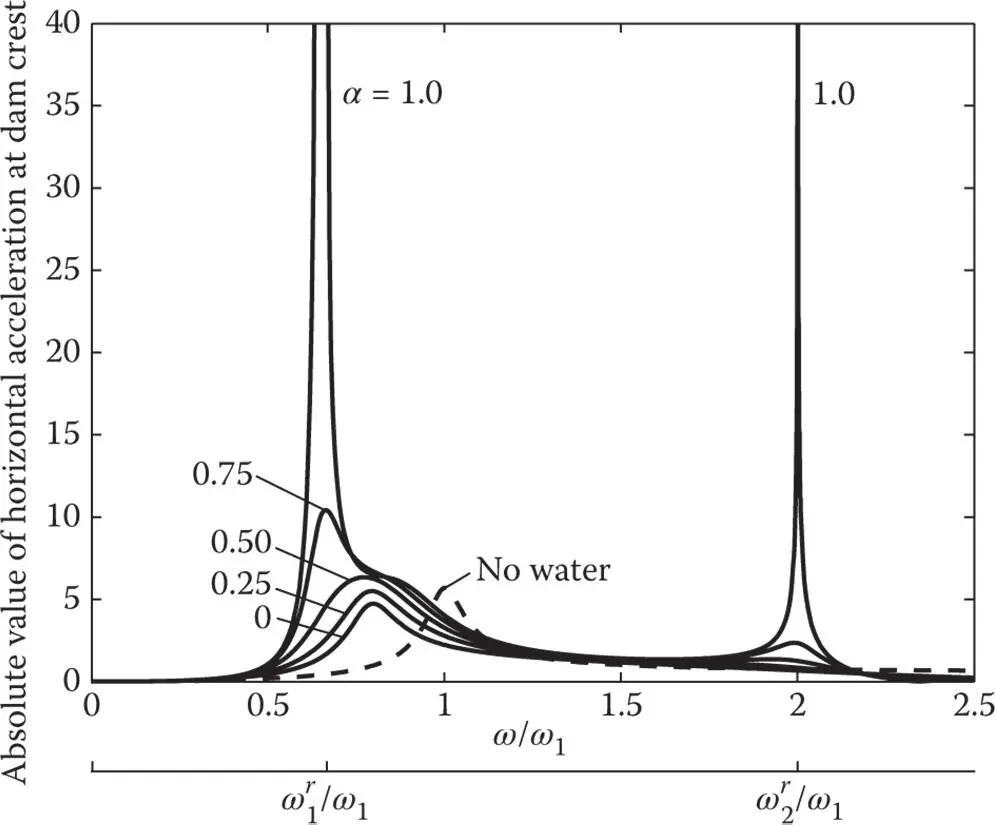
Figure 2.5.2Dam response to harmonic vertical ground motion; frequency ratio, Ω r= 0.67, i.e. E s= 5.67 million psi; α = 1.0, 0.75, 0.50, 0.25, and 0; response of dam alone is also shown.
The response function due to horizontal ground motion is especially complicated if the pressure waves are fully reflected at the reservoir bottom, i.e. α = 1, because at excitation frequencies equal to 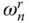 , the natural vibration frequencies of the impounded water, the added mass and force are both unbounded. When determined by a limiting process, however, the response function due to horizontal ground motion has bounded values at
, the natural vibration frequencies of the impounded water, the added mass and force are both unbounded. When determined by a limiting process, however, the response function due to horizontal ground motion has bounded values at 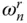 (Chopra 1968), which appear as local dips in the response curve ( Figures 2.5.1and 2.5.3).
(Chopra 1968), which appear as local dips in the response curve ( Figures 2.5.1and 2.5.3).
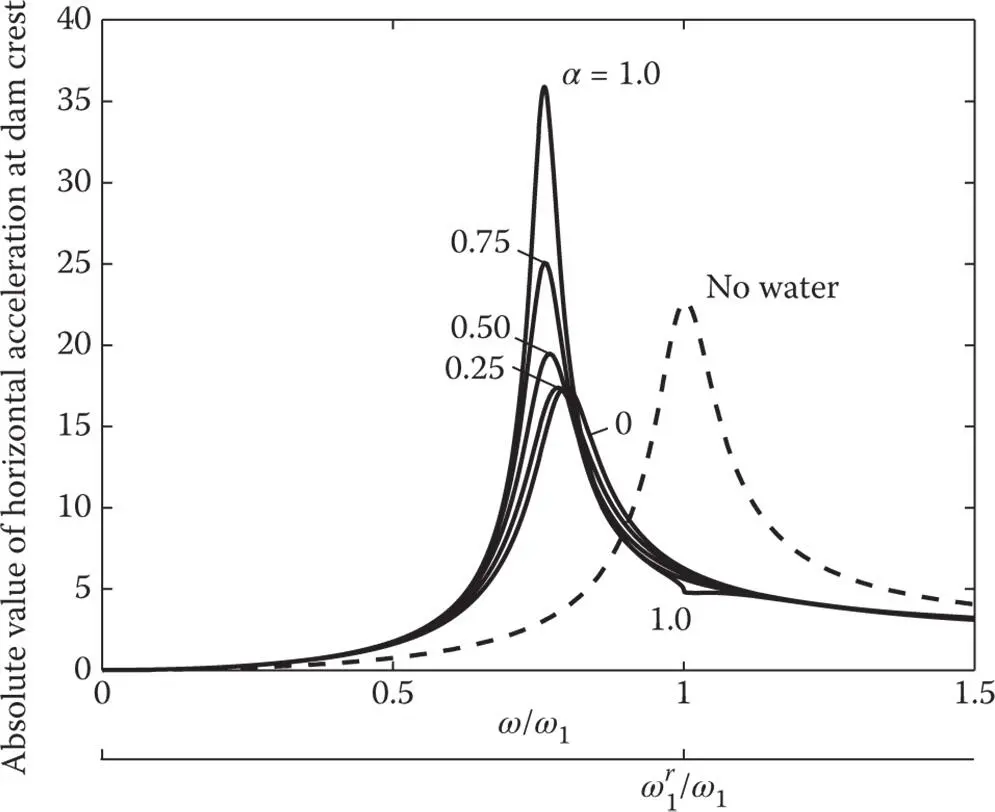
Figure 2.5.3Dam response to harmonic horizontal ground motion; frequency ratio, Ω r= 1.0, i.e. E s= 2.52 million psi; α = 1.0, 0.75, 0.50, 0.25, and 0; response of dam alone is also shown.
Figure 2.5.4Dam response to harmonic vertical ground motion; frequency ratio, Ω r= 1.0, i.e. E s= 2.52 million psi; α = 1.0, 0.75, 0.50, 0.25, and 0; response of dam alone is also shown.
The response function due to vertical ground motion also displays the first resonance at a frequency lower than the natural frequency ω 1of the dam alone with complicated behavior in the frequency range between ω 1and 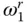 that is dominated by the unbounded response values at excitation frequencies equal to
that is dominated by the unbounded response values at excitation frequencies equal to 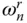 ( Figures 2.5.2and 2.5.4). These unbounded peaks are not the result of resonance in the usual sense, which is associated with the denominator in Eq. (2.4.10)attaining a minimum, but are caused by the unbounded added force. Reservoir bottom absorption reduces the added force associated with both ground motion components and the added mass to bounded values at
( Figures 2.5.2and 2.5.4). These unbounded peaks are not the result of resonance in the usual sense, which is associated with the denominator in Eq. (2.4.10)attaining a minimum, but are caused by the unbounded added force. Reservoir bottom absorption reduces the added force associated with both ground motion components and the added mass to bounded values at 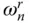 ( Section 2.3.3). Consequently, the dips at
( Section 2.3.3). Consequently, the dips at 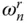 in the response function due to horizontal ground motion are eliminated; and the unbounded values at
in the response function due to horizontal ground motion are eliminated; and the unbounded values at 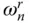 in the response function due to vertical ground motion are reduced to bounded peaks, which disappear for the smaller values of α .
in the response function due to vertical ground motion are reduced to bounded peaks, which disappear for the smaller values of α .
2.5.4 Implications of Ignoring Water Compressibility
Earthquake analysis of dams is greatly simplified if compressibility of water is ignored, because then hydrodynamic effects can be modeled by a frequency‐independent added mass ( Section 2.3.4). Here, we answer the important question: can water compressibility be ignored in the earthquake analysis of concrete gravity dams?
Frequency response curves of the dam without water, when presented using normalized scales as in Figures 2.5.5and 2.5.6, are independent of the modulus of elasticity, E s, of concrete. Similarly, the response curves including hydrodynamic effects do not vary with E sif water compressibility is ignored (Chopra 1968). However, the Ω rparameter, or correspondingly the E svalue, affects the response functions when water compressibility is included.
Читать дальше

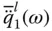 , is a dimensionless response factor representing the ratio of horizontal acceleration at the dam crest to unit free‐field ground acceleration in the l (= x or y ) direction. For each case mentioned above, the absolute value of this complex‐valued response factor is plotted against the normalized excitation frequency ω / ω 1. When presented in this form, the results apply to dams of all heights with the idealized triangular cross section, and chosen Ω r, H / H s, and α values.
, is a dimensionless response factor representing the ratio of horizontal acceleration at the dam crest to unit free‐field ground acceleration in the l (= x or y ) direction. For each case mentioned above, the absolute value of this complex‐valued response factor is plotted against the normalized excitation frequency ω / ω 1. When presented in this form, the results apply to dams of all heights with the idealized triangular cross section, and chosen Ω r, H / H s, and α values.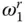 of the impounded water.
of the impounded water.

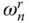 , the natural vibration frequencies of the impounded water, the added mass and force are both unbounded. When determined by a limiting process, however, the response function due to horizontal ground motion has bounded values at
, the natural vibration frequencies of the impounded water, the added mass and force are both unbounded. When determined by a limiting process, however, the response function due to horizontal ground motion has bounded values at 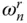 (Chopra 1968), which appear as local dips in the response curve ( Figures 2.5.1and 2.5.3).
(Chopra 1968), which appear as local dips in the response curve ( Figures 2.5.1and 2.5.3).

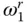 that is dominated by the unbounded response values at excitation frequencies equal to
that is dominated by the unbounded response values at excitation frequencies equal to 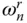 ( Figures 2.5.2and 2.5.4). These unbounded peaks are not the result of resonance in the usual sense, which is associated with the denominator in Eq. (2.4.10)attaining a minimum, but are caused by the unbounded added force. Reservoir bottom absorption reduces the added force associated with both ground motion components and the added mass to bounded values at
( Figures 2.5.2and 2.5.4). These unbounded peaks are not the result of resonance in the usual sense, which is associated with the denominator in Eq. (2.4.10)attaining a minimum, but are caused by the unbounded added force. Reservoir bottom absorption reduces the added force associated with both ground motion components and the added mass to bounded values at 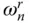 ( Section 2.3.3). Consequently, the dips at
( Section 2.3.3). Consequently, the dips at 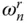 in the response function due to horizontal ground motion are eliminated; and the unbounded values at
in the response function due to horizontal ground motion are eliminated; and the unbounded values at 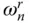 in the response function due to vertical ground motion are reduced to bounded peaks, which disappear for the smaller values of α .
in the response function due to vertical ground motion are reduced to bounded peaks, which disappear for the smaller values of α .










