If the reservoir bottom is non‐absorptive, i.e. α = 1, the hydrodynamic forces due to both ground motion components are unbounded at the natural vibration frequencies 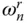 of the impounded water. The hydrodynamic force due to vertical ground motion is in‐phase or opposite‐phase relative to the ground acceleration for all excitation frequencies. The hydrodynamic force due to horizontal ground motion is of opposite‐phase relative to the ground acceleration for excitation frequencies less than the first natural vibration frequency
of the impounded water. The hydrodynamic force due to vertical ground motion is in‐phase or opposite‐phase relative to the ground acceleration for all excitation frequencies. The hydrodynamic force due to horizontal ground motion is of opposite‐phase relative to the ground acceleration for excitation frequencies less than the first natural vibration frequency 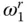 , but a 90°‐out‐of‐phase component exists for higher excitation frequencies.
, but a 90°‐out‐of‐phase component exists for higher excitation frequencies.
As mentioned earlier, the hydrodynamic pressure, Eq. (2.3.12a), and hence the total force on a rigid dam due to horizontal ground motion have been expressed as an infinite series wherein each term represents the contribution of a natural vibration mode of the impounded water. If the reservoir bottom is non‐absorptive, i.e. α = 1, the contribution of the n th mode is real‐valued with opposite‐phase relative to the ground acceleration for excitation frequencies lower than 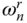 , the n th natural vibration frequency; but is imaginary‐valued, i.e. 90°‐out‐of‐phase relative to the ground acceleration, for excitation frequencies higher than
, the n th natural vibration frequency; but is imaginary‐valued, i.e. 90°‐out‐of‐phase relative to the ground acceleration, for excitation frequencies higher than 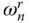 , and is unbounded when the excitation frequency is equal to
, and is unbounded when the excitation frequency is equal to 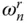 . For excitation frequencies higher than
. For excitation frequencies higher than 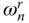 the pressure wave associated with the n th mode propagates in the upstream direction of the infinitely long fluid domain resulting in radiation of energy, As the excitation frequency increases past
the pressure wave associated with the n th mode propagates in the upstream direction of the infinitely long fluid domain resulting in radiation of energy, As the excitation frequency increases past 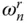 , the hydrodynamic force contribution of the n th mode changes from a pressure function decaying exponentially in the upstream direction to one propagating in the upstream direction, thus reducing the real component of
, the hydrodynamic force contribution of the n th mode changes from a pressure function decaying exponentially in the upstream direction to one propagating in the upstream direction, thus reducing the real component of 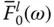 and increasing its imaginary component ( Figure 2.3.2). With increasing excitation frequency, a larger number of modes are associated with the propagating pressure waves, leading to increased energy radiation and hence smaller hydrodynamic force ( Figure 2.3.2a) – except for the local resonances at
and increasing its imaginary component ( Figure 2.3.2). With increasing excitation frequency, a larger number of modes are associated with the propagating pressure waves, leading to increased energy radiation and hence smaller hydrodynamic force ( Figure 2.3.2a) – except for the local resonances at 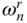 ; these unbounded resonances are unrealistic artifacts of a non‐absorptive boundary at the reservoir bottom.
; these unbounded resonances are unrealistic artifacts of a non‐absorptive boundary at the reservoir bottom.
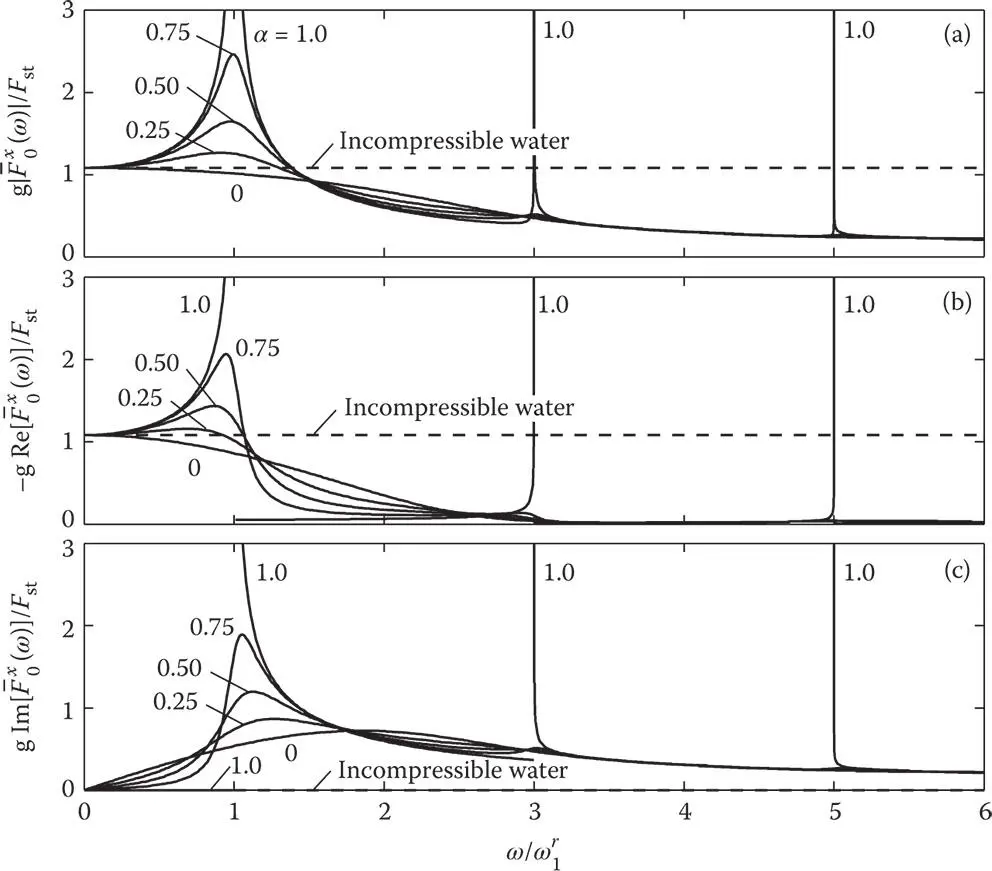
Figure 2.3.2Hydrodynamic force on rigid dam due to horizontal ground acceleration: (a) absolute value; (b) real component; and (c) imaginary component.
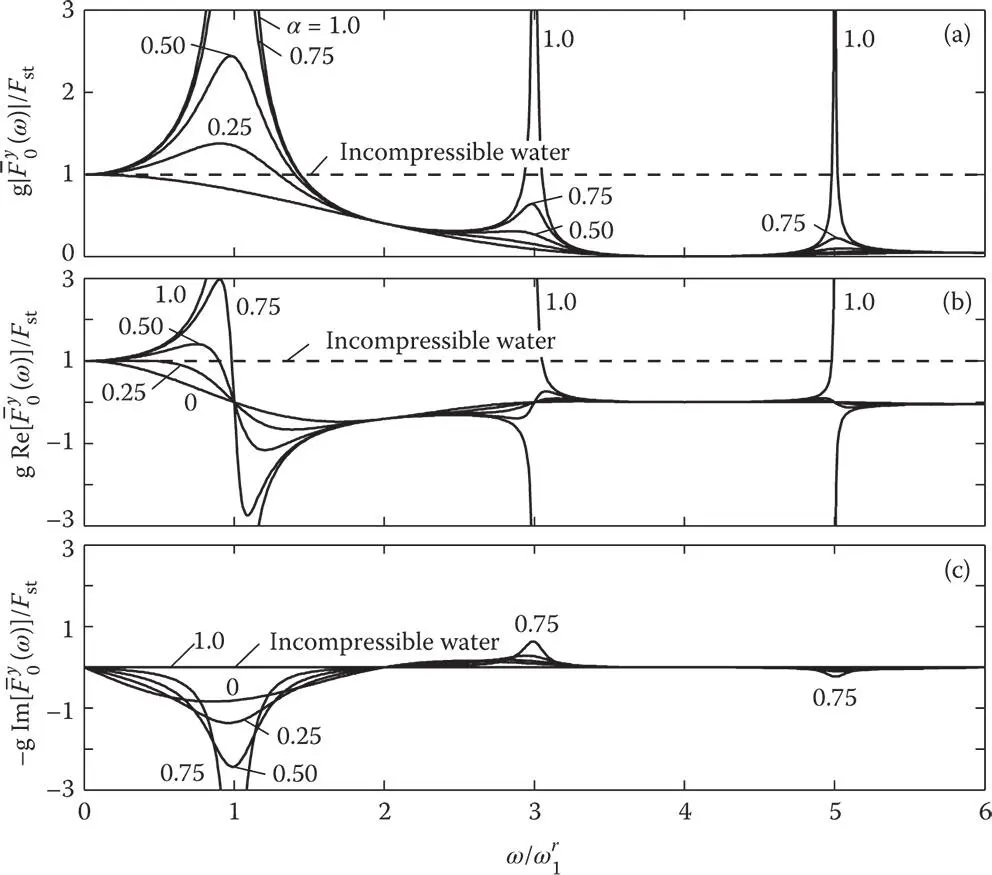
Figure 2.3.3Hydrodynamic force on rigid dam due to vertical ground acceleration: (a) absolute value; (b) real component; and (c) imaginary component.
For an absorptive reservoir bottom, the frequency‐dependent eigenvalues μ n( ω ) of the impounded water are complex‐valued for all excitation frequencies. Consequently, the contribution of the n th natural vibration mode of the impounded water to the hydrodynamic force due to horizontal ground motion is complex‐valued for all excitation frequencies; wherein the imaginary (or 90°‐out‐of‐phase) component arises from the radiation of energy due to propagation of pressure waves in the upstream direction and their refraction into the reservoir bottom. This implies that if the reservoir bottom is absorptive, the hydrodynamic force contains a 90°‐out‐of‐phase component even for excitation frequencies lower than 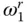 ( Figure 2.3.2c). Because of the additional energy loss resulting from wave absorption at the reservoir bottom, the hydrodynamic force is bounded for all excitation frequencies, the fundamental resonant peak is reduced, and the higher resonant peaks are virtually eliminated. However, the additional energy absorption into the reservoir bottom has little influence on the natural frequencies of the impounded water.
( Figure 2.3.2c). Because of the additional energy loss resulting from wave absorption at the reservoir bottom, the hydrodynamic force is bounded for all excitation frequencies, the fundamental resonant peak is reduced, and the higher resonant peaks are virtually eliminated. However, the additional energy absorption into the reservoir bottom has little influence on the natural frequencies of the impounded water.
The hydrodynamic pressure due to vertical ground motion is independent of the upstream coordinate (Chopra 1967) and the pressure waves do not propagate in the upstream direction, resulting in a truly undamped system if the reservoir bottom is non‐absorptive. The hydrodynamic pressure is real‐valued, in‐phase, or opposite‐phase relative to the ground acceleration, for all excitation frequencies. Energy loss associated with refraction of pressure waves into a flexible bottom leads to an imaginary component for all excitation frequencies. This energy loss reduces the response at all frequencies and the resonant responses are now bounded.
If water compressibility is neglected, the frequency response functions for hydrodynamic pressure on a rigid dam, given by Eqs. (2.3.20)and (2.3.21), are real‐valued and independent of the excitation frequency ( Figures 2.3.2and 2.3.3). The hydrodynamic force due to vertical ground motion is equal to the hydrostatic force ( Figure 2.3.3), and in‐phase with the ground acceleration; whereas the hydrodynamic force due to horizontal ground motion is slightly larger than the hydrostatic force ( Figure 2.3.2), and has opposite‐phase relative to the ground acceleration.
2.3.4 Westergaard's Results and Added Mass Analogy
In 1933 Westergaard derived an equation for the hydrodynamic pressure on the upstream face of a rigid dam due to time‐harmonic horizontal ground motion, a result that for several decades profoundly influenced the treatment of hydrodynamic effects in dam analysis. The range of validity of this result will be identified in this section. His result for hydrodynamic pressure on the upstream face of the dam due to 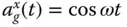 , expressed in the Cartesian coordinate system and notation adopted herein, is
, expressed in the Cartesian coordinate system and notation adopted herein, is
(2.3.22) 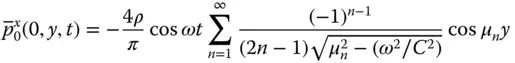
To evaluate this classical result, we substitute Eq. (2.3.18)in Eq. (2.3.7), and separate the real part to obtain the hydrodynamic pressure due to the excitation 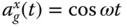 :
:
Читать дальше

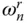 of the impounded water. The hydrodynamic force due to vertical ground motion is in‐phase or opposite‐phase relative to the ground acceleration for all excitation frequencies. The hydrodynamic force due to horizontal ground motion is of opposite‐phase relative to the ground acceleration for excitation frequencies less than the first natural vibration frequency
of the impounded water. The hydrodynamic force due to vertical ground motion is in‐phase or opposite‐phase relative to the ground acceleration for all excitation frequencies. The hydrodynamic force due to horizontal ground motion is of opposite‐phase relative to the ground acceleration for excitation frequencies less than the first natural vibration frequency 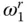 , but a 90°‐out‐of‐phase component exists for higher excitation frequencies.
, but a 90°‐out‐of‐phase component exists for higher excitation frequencies.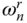 , the n th natural vibration frequency; but is imaginary‐valued, i.e. 90°‐out‐of‐phase relative to the ground acceleration, for excitation frequencies higher than
, the n th natural vibration frequency; but is imaginary‐valued, i.e. 90°‐out‐of‐phase relative to the ground acceleration, for excitation frequencies higher than 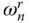 , and is unbounded when the excitation frequency is equal to
, and is unbounded when the excitation frequency is equal to 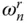 . For excitation frequencies higher than
. For excitation frequencies higher than 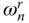 the pressure wave associated with the n th mode propagates in the upstream direction of the infinitely long fluid domain resulting in radiation of energy, As the excitation frequency increases past
the pressure wave associated with the n th mode propagates in the upstream direction of the infinitely long fluid domain resulting in radiation of energy, As the excitation frequency increases past 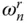 , the hydrodynamic force contribution of the n th mode changes from a pressure function decaying exponentially in the upstream direction to one propagating in the upstream direction, thus reducing the real component of
, the hydrodynamic force contribution of the n th mode changes from a pressure function decaying exponentially in the upstream direction to one propagating in the upstream direction, thus reducing the real component of 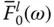 and increasing its imaginary component ( Figure 2.3.2). With increasing excitation frequency, a larger number of modes are associated with the propagating pressure waves, leading to increased energy radiation and hence smaller hydrodynamic force ( Figure 2.3.2a) – except for the local resonances at
and increasing its imaginary component ( Figure 2.3.2). With increasing excitation frequency, a larger number of modes are associated with the propagating pressure waves, leading to increased energy radiation and hence smaller hydrodynamic force ( Figure 2.3.2a) – except for the local resonances at 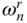 ; these unbounded resonances are unrealistic artifacts of a non‐absorptive boundary at the reservoir bottom.
; these unbounded resonances are unrealistic artifacts of a non‐absorptive boundary at the reservoir bottom.

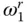 ( Figure 2.3.2c). Because of the additional energy loss resulting from wave absorption at the reservoir bottom, the hydrodynamic force is bounded for all excitation frequencies, the fundamental resonant peak is reduced, and the higher resonant peaks are virtually eliminated. However, the additional energy absorption into the reservoir bottom has little influence on the natural frequencies of the impounded water.
( Figure 2.3.2c). Because of the additional energy loss resulting from wave absorption at the reservoir bottom, the hydrodynamic force is bounded for all excitation frequencies, the fundamental resonant peak is reduced, and the higher resonant peaks are virtually eliminated. However, the additional energy absorption into the reservoir bottom has little influence on the natural frequencies of the impounded water.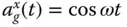 , expressed in the Cartesian coordinate system and notation adopted herein, is
, expressed in the Cartesian coordinate system and notation adopted herein, is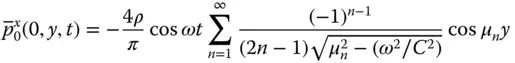
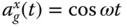 :
:










