Anil K. Chopra - Earthquake Engineering for Concrete Dams
Здесь есть возможность читать онлайн «Anil K. Chopra - Earthquake Engineering for Concrete Dams» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Earthquake Engineering for Concrete Dams
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Earthquake Engineering for Concrete Dams: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Earthquake Engineering for Concrete Dams»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
offers a comprehensive, integrated view of this progress over the last fifty years. The book offers an understanding of the limitations of the various methods of dynamic analysis used in practice and develops modern methods that overcome these limitations.
This important book:
Develops procedures for dynamic analysis of two-dimensional and three-dimensional models of concrete dams Identifies system parameters that influence their response Demonstrates the effects of dam–water–foundation interaction on earthquake response Identifies factors that must be included in earthquake analysis of concrete dams Examines design earthquakes as defined by various regulatory bodies and organizations Presents modern methods for establishing design spectra and selecting ground motions Illustrates application of dynamic analysis procedures to the design of new dams and safety evaluation of existing dams. Written for graduate students, researchers, and professional engineers,
offers a comprehensive view of the current procedures and methods for seismic analysis, design, and safety evaluation of concrete dams.

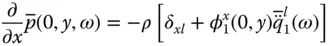
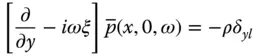
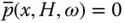
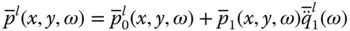
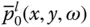 and
and 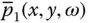 were presented in Eq. (2.3.12).
were presented in Eq. (2.3.12).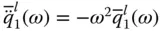 into Eq. (2.4.6)leads to the frequency response function for the fundamental modal coordinate when the dam is subjected to the l ‐component of ground motion ( l = x , y ):
into Eq. (2.4.6)leads to the frequency response function for the fundamental modal coordinate when the dam is subjected to the l ‐component of ground motion ( l = x , y ):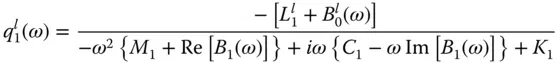
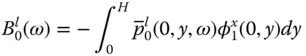
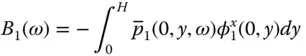
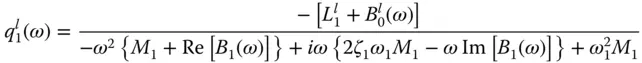
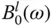 , and modifying the properties of the dam by an added mass represented by the real component of B 1( ω ), and an added damping represented by the imaginary component B 1( ω ). The added mass arises from the portion of the impounded water that reacts in phase with the motion of the dam, and the added damping arises from radiation of pressure waves in the upstream direction and from their refraction into the absorptive reservoir bottom.
, and modifying the properties of the dam by an added mass represented by the real component of B 1( ω ), and an added damping represented by the imaginary component B 1( ω ). The added mass arises from the portion of the impounded water that reacts in phase with the motion of the dam, and the added damping arises from radiation of pressure waves in the upstream direction and from their refraction into the absorptive reservoir bottom.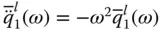 for a dam with a fixed cross‐sectional geometry and Poisson's ratio, when expressed as a function of the normalized excitation frequency ω / ω 1, depends on three system parameters:
for a dam with a fixed cross‐sectional geometry and Poisson's ratio, when expressed as a function of the normalized excitation frequency ω / ω 1, depends on three system parameters: 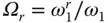 , the ratio of the fundamental natural vibration frequency of the impounded water to that of the dam alone; H / H s, the ratio of water depth to the dam height; and α , the wave reflection coefficient at the reservoir bottom (Chopra 1968). We know that
, the ratio of the fundamental natural vibration frequency of the impounded water to that of the dam alone; H / H s, the ratio of water depth to the dam height; and α , the wave reflection coefficient at the reservoir bottom (Chopra 1968). We know that 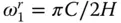 ( Eq. (2.3.16)), and it can be shown that ω 1= γC s/ H s, where γ is a dimensionless factor that depends on the cross‐sectional shape of the dam monolith and the Poisson's ratio of the concrete in the dam,
( Eq. (2.3.16)), and it can be shown that ω 1= γC s/ H s, where γ is a dimensionless factor that depends on the cross‐sectional shape of the dam monolith and the Poisson's ratio of the concrete in the dam, 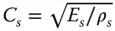 , E sis the Young's modulus, and ρ sis the density of concrete. Therefore
, E sis the Young's modulus, and ρ sis the density of concrete. Therefore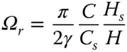
 . Thus Ω rdecreases with increasing E sor dam stiffness, and vice versa.
. Thus Ω rdecreases with increasing E sor dam stiffness, and vice versa.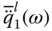 , when expressed as a function of ω / ω 1, is independent of E s, and α ; the incompressible case implies C = ∞ and thus Ω r= ∞.
, when expressed as a function of ω / ω 1, is independent of E s, and α ; the incompressible case implies C = ∞ and thus Ω r= ∞.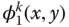 were determined using a finite element idealization of the dam, and the integrals involved in M 1,
were determined using a finite element idealization of the dam, and the integrals involved in M 1, 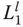 ,
, 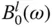 , and B 1( ω ) were computed in discretized form.
, and B 1( ω ) were computed in discretized form.










