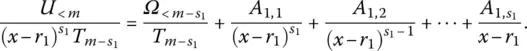F. Xavier Malcata - Mathematics for Enzyme Reaction Kinetics and Reactor Performance
Здесь есть возможность читать онлайн «F. Xavier Malcata - Mathematics for Enzyme Reaction Kinetics and Reactor Performance» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Mathematics for Enzyme Reaction Kinetics and Reactor Performance
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Mathematics for Enzyme Reaction Kinetics and Reactor Performance: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Mathematics for Enzyme Reaction Kinetics and Reactor Performance»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Enzyme Reactor Engineering
The second volume begins with an introduction to basic concepts in calculus, i.e. limits, derivatives, integrals and differential equations; limits, along with continuity, are further expanded afterwards, covering uni- and multivariate cases, as well as classical theorems. After recovering the concept of differential and applying it to generate (regular and partial) derivatives, the most important rules of differentiation of functions, in explicit, implicit and parametric form, are retrieved – together with the nuclear theorems supporting simpler manipulation thereof. The book then tackles strategies to optimize uni- and multivariate functions, before addressing integrals in both indefinite and definite forms. Next, the book touches on the methods of solution of differential equations for practical applications, followed by analytical geometry and vector calculus. Brief coverage of statistics–including continuous probability functions, statistical descriptors and statistical hypothesis testing, brings the second volume to a close.

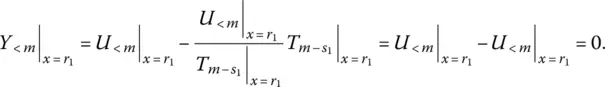
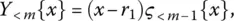
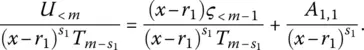
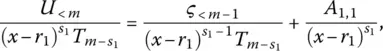
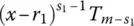 is again a regular rational fraction, because the degree of ς { x } is lower than m − 1 (as indicated by the subscript utilized) – while the degree of the corresponding polynomial in denominator equals s 1– 1 + ( m − s 1) = m − 1, on account of the degree s 1− 1 of
is again a regular rational fraction, because the degree of ς { x } is lower than m − 1 (as indicated by the subscript utilized) – while the degree of the corresponding polynomial in denominator equals s 1– 1 + ( m − s 1) = m − 1, on account of the degree s 1− 1 of 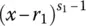 and the degree m − s 1of
and the degree m − s 1of 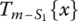 . Therefore, one may proceed to another splitting step of the type
. Therefore, one may proceed to another splitting step of the type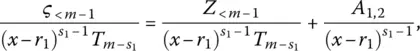
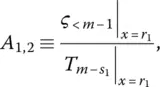
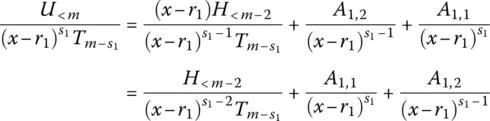
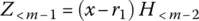 , following Eqs. (2.199)and (2.200)as template. This method may undergo up to s 1iterations, to eventually produce
, following Eqs. (2.199)and (2.200)as template. This method may undergo up to s 1iterations, to eventually produce