1 Cover
2 About the Author
3 Series Preface
4 Preface
5 Volume 1 1 Basic Concepts of Algebra 1 Scalars, Vectors, Matrices, and Determinants 2 Function Features 2.1 Series 2.2 Multiplication and Division of Polynomials 2.3 Trigonometric Functions 2.4 Hyperbolic Functions 3 Vector Operations 3.1 Addition of Vectors 3.2 Multiplication of Scalar by Vector 3.3 Scalar Multiplication of Vectors 3.4 Vector Multiplication of Vectors 4 Matrix Operations 4.1 Addition of Matrices 4.2 Multiplication of Scalar by Matrix 4.3 Multiplication of Matrices 4.4 Transposal of Matrices 4.5 Inversion of Matrices 4.6 Combined Features 5 Tensor Operations 6 Determinants 6.1 Definition 6.2 Calculation 6.3 Eigenvalues and Eigenvectors 7 Solution of Algebraic Equations 7.1 Linear Systems of Equations 7.2 Quadratic Equation 7.3 Lambert’s W Function 7.4 Numerical Approaches
6 Further Reading
7 Volume 2 About the Author Series Preface Preface 2 Basic Concepts of Calculus 8 Limits, Derivatives, Integrals, and Differential Equations 9 Limits and Continuity 9.1 Univariate Limit 9.2 Multivariate Limit 9.3 Basic Theorems on Limits 9.4 Definition of Continuity 9.5 Basic Theorems on Continuity 10 Differentials, Derivatives, and Partial Derivatives 10.1 Differential 10.2 Derivative 10.3 Dependence Between Functions 10.4 Optimization of Univariate Continuous Functions 10.5 Optimization of Multivariate Continuous Functions 11 Integrals 11.1 Univariate Integral 11.2 Multivariate Integral 11.3 Optimization of Single Integral 11.4 Optimization of Set of Derivatives 12 Infinite Series and Integrals 12.1 Definition and Criteria of Convergence 12.2 Taylor’s Series 12.3 Gamma Function and Factorial 13 Analytical Geometry 13.1 Straight Line 13.2 Simple Polygons 13.3 Conical Curves 13.4 Length of Line 13.5 Curvature of Line 13.6 Area of Plane Surface 13.7 Outer Area of Revolution Solid 13.8 Volume of Revolution Solid 14 Transforms 14.1 Laplace’s Transform 14.2 Legendre’s Transform 15 Solution of Differential Equations 15.1 Ordinary Differential Equations 15.2 Partial Differential Equations 16 Vector Calculus 16.1 Rectangular Coordinates 16.2 Cylindrical Coordinates 16.3 Spherical Coordinates 16.4 Curvature of Three‐dimensional Surfaces 16.5 Three‐dimensional Integration 17 Numerical Approaches to Integration 17.1 Calculation of Definite Integrals 17.2 Integration of Differential Equations 3 Basic Concepts of Statistics 18 Continuous Probability Functions 18.1 Basic Statistical Descriptors 18.2 Normal Distribution 18.3 Other Relevant Distributions 19 Statistical Hypothesis Testing 20 Linear Regression 20.1 Parameter Fitting 20.2 Residual Characterization 20.3 Parameter Inference 20.4 Unbiased Estimation 20.5 Prediction Inference 20.6 Multivariate Correction
8 Further Reading
9 Index
10 End User License Agreement
1 Chapter 2 Table 2.1 Pascal’s triangle encompassing coefficients of power of binomial, 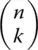 ,...
,...
2 Chapter 7Table 7.1 Nature of roots of set of m linear equations in n unknowns, as a fun...
3 Chapter 10Table 10.1 List of derivatives obtained via definition.Table 10.2 List of derivatives obtained via theorem of sum of functions.Table 10.3 List of derivatives obtained via the theorem on product of functio...Table 10.4 List of derivatives obtained via the theorem of quotient of functi...Table 10.5 List of derivatives obtained via theorem of inverse function.Table 10.6 List of derivatives obtained via theorem of composite function.
4 Chapter 11Table 11.1 List of elementary indefinite integrals.Table 11.2 List of indefinite integrals obtained by rule of decomposition.Table 11.3 List of indefinite integrals obtained by rule of integration by pa...Table 11.4 List of indefinite integrals obtained by rule of integration by ch...
5 Chapter 12Table 12.1 Actual values, and Stirling’s approximants of factorials of the fi...
6 Chapter 14Table 14.1 List of Laplace’s transforms of functions obtained via definitionTable 14.2 List of Laplace’s transforms of functions obtained via associated ...Table 14.3 List of Laplace’s inverse transforms of functions obtained via def...
7 Chapter 15Table 15.1 Nature of critical points, and qualitative features of eigenvalues...Table 15.2 Combination of values of i = 0, 1, 2 , … and j = 0, 1 , … ...
8 Chapter 17Table 17.1 List of (integer) coefficients H n,jand 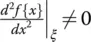 H , n,j, each associated to...Table 17.2 Characteristic coefficients, a s – j( j = 1, 2, …...Table 17.3 Characteristic coefficients, a s − j( j = 1, 2, …, s Table 17.4 List of order of accuracy, p , and associated minimum number of stages,...
H , n,j, each associated to...Table 17.2 Characteristic coefficients, a s – j( j = 1, 2, …...Table 17.3 Characteristic coefficients, a s − j( j = 1, 2, …, s Table 17.4 List of order of accuracy, p , and associated minimum number of stages,...
9 Chapter 18Table 18.1 Critical, unilateral and bilateral, quantiles of (standard normal)Table 18.2 Critical, unilateral and bilateral, quantiles of chi‐square‐statis...Table 18.3 Critical, unilateral and bilateral, quantiles of t -statistic, t crt,...Table 18.4 Critical, unilateral and bilateral, quantiles of F ‐statistic, F crt,...
10 Chapter 19Table 19.1 Description of types of statistical errors and (given) critical va...Table 19.2 Most common statistical tests, and associated features in terms of...
1 Chapter 2 Figure 2.1 Variation of absolute value, | x |, as a function of a real number,... Figure 2.2 Variation of (natural) (a) exponential, e x, and (b) logarithm, ln... Figure 2.3 Variation of arithmetic mean ( arm ), logarithmic mean ( lom ), geome... Figure 2.4 Variation of value of n ‐term arithmetic series, S n, normalized by... Figure 2.5 Variation of value of n ‐term geometric series, S n, normalized by ... Figure 2.6 Variation of value of n ‐term arithmetic–geometric series, S n, nor... Figure 2.7 Graphical algorithm of (long) Euclidean division of polynomials o... Figure 2.8 Graphical algorithm of (long) Ruffini’s division of polynomials –... Figure 2.9 Geometric demonstration of Newton’s binomial formula at two dimen... Figure 2.10 (a) Trigonometric circle, described by vector u of unit length c... Figure 2.11 Illustration of Pythagoras’ theorem as (a) graphical statement, ... Figure 2.12 Graphical representation of generic triangle [ ABC ] – with indica... Figure 2.13 Variation, with their argument x , of major inverse trigonometric... Figure 2.14 Variation, with their argument x , of major hyperbolic functions,... Figure 2.15 Variation, with their argument x , of inverse hyperbolic function...
2 Chapter 3 Figure 3.1 Graphical representation of (a) addition of two vectors, uand v,... Figure 3.2 Graphical representation of (a) vectors u, v, and w, and of sum, Figure 3.3 Graphical representation of (a) vectors u and v , (b) u and symmet... Figure 3.4 Graphical representation of (a) vectors u, v, and w, and of sum,
3 Chapter 6 Figure 6.1 Graphical representation of vectors uand v, (a) with coordinates...
4 Chapter 7Figure 7.1 Graphical solution of quadratic equation ax 2 + bx + c = ...Figure 7.2 Variation, with its argument x , of Lambert’s W function within th...Figure 7.3 Evolution in root searching for equation f { x } = 0 via bisection ...Figure 7.4 Evolution in root searching for equation f { x } = 0 via linear int...Figure 7.5 Evolution in root searching for equation f { x } = 0 via Newton and...Figure 7.6 Evolution in root searching for equation f { x } = 0 via secant met...Figure 7.7 Evolution in root searching for equation f { x } = 0 via direct ite...
Читать дальше

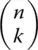 ,...
,...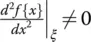 H , n,j, each associated to...Table 17.2 Characteristic coefficients, a s – j( j = 1, 2, …...Table 17.3 Characteristic coefficients, a s − j( j = 1, 2, …, s Table 17.4 List of order of accuracy, p , and associated minimum number of stages,...
H , n,j, each associated to...Table 17.2 Characteristic coefficients, a s – j( j = 1, 2, …...Table 17.3 Characteristic coefficients, a s − j( j = 1, 2, …, s Table 17.4 List of order of accuracy, p , and associated minimum number of stages,...










