These constructions can be easily generalized to multiple predictors, with different variations of models obtainable. For example, a regression model with unequal slopes for some predictors and equal slopes for others is fit by including products of the indicator and the predictor for the ones with different slopes and not including them for the predictors with equal slopes. Appropriate 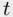 ‐ and
‐ and 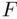 ‐tests can then be constructed to make particular comparisons of models.
‐tests can then be constructed to make particular comparisons of models.
A reasonable question to ask at this point is “Why bother to fit the full model? Isn't it just the same as fitting two separate regressions on the two groups?” The answer is no. The full model fit above assumes that the variance of the errors is the same (the constant variance assumption), while fitting two separate regressions allows the variances to be different. The fitted slope coefficients from the full model will, however, be identical to those from two separate fits. What is gained by analyzing the data this way is the comparison of versions of pooled, constant shift, and full models based on group membership, including different slopes for some variables and equal slopes for others, something that is not possible if separate regressions are fit to the two groups.
Another way of saying that the relationship between a predictor and the target is different for members of the two different groups is that there is an interaction effectbetween the predictor and group membership on the target. Social scientists would say that the grouping has a moderating effect on the relationship between the predictor and the target. The fact that in the case of a grouping variable, the interaction can be fit by multiplying the two variables together has led to a practice that is common in some fields: to try to represent any interaction between variables (that is, any situation where the relationship between a predictor and the target is different for different values of another predictor) by multiplying them together. Unfortunately, this is not a very reasonable way to think about interactions for numerical predictors, since there are many ways that the effect of one variable on the target can differ depending on the value of another that have nothing to do with product functions. See Section 15.6 for further discussion.
2.4.1 EXAMPLE — ELECTRONIC VOTING AND THE 2004 PRESIDENTIAL ELECTION
The 2000 US presidential election matching Republican George W. Bush against Democrat Al Gore attracted worldwide attention because of its close and controversial results, particularly in the state of Florida. The 2004 election, pitting the incumbent Bush against John Kerry, is less discussed, but was also controversial, in part because of the introduction of electronic voting machines in some polling places across the country (such machines were introduced in part because of the irregularities in paper balloting that occurred in Florida in the 2000 election). Some of the manufacturers of electronic voting machines were strong supporters of President Bush, and this, along with the fact that the machines did not produce a paper trail, led to speculation about whether the machines could be manipulated to favor one candidate over the other.

FIGURE 2.4: Plots for the 2004 election data. (a) Plot of percentage change in Bush vote versus 2000 Bush vote. (b) Side‐by‐side boxplots of percentage change in Bush vote by whether or not the county employed electronic voting in 2004.
This analysis is based on data from Hout et al. (2004) (see also Theus and Urbanek, 2009). The observations are the 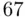 counties of Florida. Although this is not a sample of Florida counties (it is actually a census of all of them), these counties can be considered a sample of all of the counties in the country, making inferences drawn about the larger population of counties based on this set of counties meaningful. The target variable is the change in the percentage of votes cast for Bush from 2000 to 2004 (a positive number meaning a higher percentage in 2004). We start with the simple regression model relating the change in Bush percentage to the percentage of votes Bush took in 2000, with corresponding scatter plot given in the left plot of Figure 2.4. It can be seen that most of the changes are positive, reflecting that Bush carried the state by more than
counties of Florida. Although this is not a sample of Florida counties (it is actually a census of all of them), these counties can be considered a sample of all of the counties in the country, making inferences drawn about the larger population of counties based on this set of counties meaningful. The target variable is the change in the percentage of votes cast for Bush from 2000 to 2004 (a positive number meaning a higher percentage in 2004). We start with the simple regression model relating the change in Bush percentage to the percentage of votes Bush took in 2000, with corresponding scatter plot given in the left plot of Figure 2.4. It can be seen that most of the changes are positive, reflecting that Bush carried the state by more than 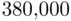 votes in 2004, compared with the very close result (a
votes in 2004, compared with the very close result (a 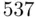 vote margin) in 2000.
vote margin) in 2000.
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -2.9968 2.0253 -1.480 0.14379 Bush.pct.2000 0.1190 0.0355 3.352 0.00134 ** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.693 on 65 degrees of freedom Multiple R-squared: 0.1474, Adjusted R-squared: 0.1343 F-statistic: 11.24 on 1 and 65 DF, p-value: 0.00134
There is a weak, but statistically significant, relationship between 2000 Bush vote and the change in vote to 2004, with counties that went more strongly for Bush in 2000 gaining more in 2004. The constant shift model now adds an indicator variable for whether a county used electronic voting in 2004. The side‐by‐side boxplots in the right plot in Figure 2.4show that overall the 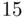 counties that used electronic voting had smaller gains for Bush than the
counties that used electronic voting had smaller gains for Bush than the 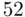 that did not, but that of course does not take the 2000 Bush vote into account. There are also signs of nonconstant variance, as the variability is smaller among the counties that used electronic voting.
that did not, but that of course does not take the 2000 Bush vote into account. There are also signs of nonconstant variance, as the variability is smaller among the counties that used electronic voting.
Coefficients: Estimate Std. Error t value Pr(>|t|) VIF (Intercept) -2.12713 2.10315 -1.011 0.31563 Bush.pct.2000 0.10804 0.03609 2.994 0.00391 1.049 ** e.Voting -1.12840 0.80218 -1.407 0.16437 1.049 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.672 on 64 degrees of freedom Multiple R-squared: 0.173, Adjusted R-squared: 0.1471 F-statistic: 6.692 on 2 and 64 DF, p-value: 0.002295
It can be seen that there is only weak (if any) evidence that the constant shift model provides improved performance over the pooled model. This does not mean that electronic voting is irrelevant, however, as it could be that two separate (unrestricted) lines are preferred.
Coefficients: Estimate Std.Error t value Pr(>|t|) VIF (Intercept) -5.23862 2.35084 -2.228 0.029431 * Bush.pct.2000 0.16228 0.04051 4.006 0.000166 1.44 *** e.Voting 9.67236 4.26530 2.268 0.026787 32.26 * Bush.2000 X e.Voting -0.20051 0.07789 -2.574 0.012403 31.10 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 2.562 on 63 degrees of freedom Multiple R-squared: 0.2517, Adjusted R-squared: 0.2161 F-statistic: 7.063 on 3 and 63 DF, p-value: 0.0003626
The 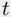 ‐test for the product variable indicates that the model with two unrestricted lines is preferred over the model with two parallel lines. A partial
‐test for the product variable indicates that the model with two unrestricted lines is preferred over the model with two parallel lines. A partial 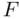 ‐test comparing this model to the pooled model, which is
‐test comparing this model to the pooled model, which is 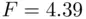 (
( 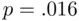 ), also supports two distinct lines,
), also supports two distinct lines,
Читать дальше

 ‐ and
‐ and 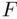 ‐tests can then be constructed to make particular comparisons of models.
‐tests can then be constructed to make particular comparisons of models.
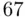 counties of Florida. Although this is not a sample of Florida counties (it is actually a census of all of them), these counties can be considered a sample of all of the counties in the country, making inferences drawn about the larger population of counties based on this set of counties meaningful. The target variable is the change in the percentage of votes cast for Bush from 2000 to 2004 (a positive number meaning a higher percentage in 2004). We start with the simple regression model relating the change in Bush percentage to the percentage of votes Bush took in 2000, with corresponding scatter plot given in the left plot of Figure 2.4. It can be seen that most of the changes are positive, reflecting that Bush carried the state by more than
counties of Florida. Although this is not a sample of Florida counties (it is actually a census of all of them), these counties can be considered a sample of all of the counties in the country, making inferences drawn about the larger population of counties based on this set of counties meaningful. The target variable is the change in the percentage of votes cast for Bush from 2000 to 2004 (a positive number meaning a higher percentage in 2004). We start with the simple regression model relating the change in Bush percentage to the percentage of votes Bush took in 2000, with corresponding scatter plot given in the left plot of Figure 2.4. It can be seen that most of the changes are positive, reflecting that Bush carried the state by more than 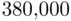 votes in 2004, compared with the very close result (a
votes in 2004, compared with the very close result (a 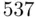 vote margin) in 2000.
vote margin) in 2000.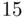 counties that used electronic voting had smaller gains for Bush than the
counties that used electronic voting had smaller gains for Bush than the 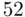 that did not, but that of course does not take the 2000 Bush vote into account. There are also signs of nonconstant variance, as the variability is smaller among the counties that used electronic voting.
that did not, but that of course does not take the 2000 Bush vote into account. There are also signs of nonconstant variance, as the variability is smaller among the counties that used electronic voting.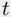 ‐test for the product variable indicates that the model with two unrestricted lines is preferred over the model with two parallel lines. A partial
‐test for the product variable indicates that the model with two unrestricted lines is preferred over the model with two parallel lines. A partial 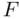 ‐test comparing this model to the pooled model, which is
‐test comparing this model to the pooled model, which is 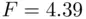 (
( 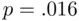 ), also supports two distinct lines,
), also supports two distinct lines,










