A. Gouveia Oliveira - Biostatistics Decoded

Now, if the original piece of cloth had large, repetitive patterns but the sample was only a tiny piece, by looking at the sample one would not be able to tell exactly what the original piece was like. This is because not every pattern and color would be present in the sample, and the sample would be said not to be representative of the original cloth. Conversely, if the sample was large enough to contain all the patterns and colors present in the piece, the sample would be said to be representative ( Figure 1.6).

This is very much the reasoning behind the classical approach to sampling. The concept of representativenessof a sample was tightly linked to its size: large samples tend to be representative, while small samples give unreliable results because they are not representative of the population. The fragility of this approach, however, is its lack of objectivity in the definition of an adequate sample size.

Figure 1.5 Classical view of the purpose of sampling.

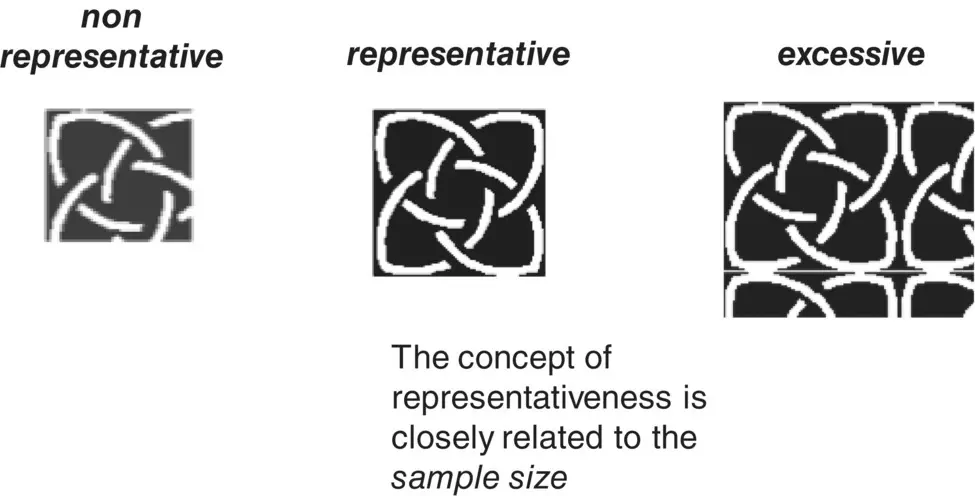
Figure 1.6 Relationship between representativeness and sample size in the classic view of sampling. The concept of representativeness is closely related to sample size.

Some people might say that the sample size should be in proportion to the total population. If so, this would mean that an investigation on the prevalence of, say, chronic heart failure in Norway would require a much smaller sample than the same investigation in Germany. This makes little sense. Now suppose we want to investigate patients with chronic heart failure. Would a sample of 100 patients with chronic heart failure be representative? What about 400 patients? Or do we need 1000 patients? In each case, the sample size is always an almost insignificant fraction of the whole population.

If it does not make much sense to think that the ideal sample size is a certain proportion of the population (even more so because in many situations the population size is not even known), would a representative sample then be the one that contains all the patterns that exist in the population? If so, how many people will we have to sample to make sure that all possible patterns in the population also exist in the sample? For example, some findings typical of chronic heart failure, like an S3‐gallop and alveolar edema, are present in only 2 or 3% of patients, and the combination of these two findings (assuming they are independent) should exist in only 1 out of 2500 patients. Does this mean that no study of chronic heart failure with less than 2500 patients should be considered representative? And what to do when the structure of the population is unknown?

The problem of lack of objectivity in defining sample representativeness can be circumvented if we adopt a different reasoning when dealing with samples. Let us accept that we have no means of knowing what the population structure truly is, and all we can possibly have is a sample of the population. Then, a realistic procedure would be to look at the sample and, by inspecting its structure, formulate a hypothesis about the structure of the population. The structure of the sample constrains the hypothesis to be consistent with the observations.

Taking the above example on the samples of cloth, the situation now is as if we were given a sample of cloth and asked what the whole piece would be like. If the sample were large, we probably would have no difficulty answering that question. But if the sample were small, something could still be said about the piece. For example, if the sample contained only red circles over a yellow background, one could say that the sample probably did not come from a Persian carpet. In other words, by inspecting the sample one could say that it was consistent with a number of pieces of cloth but not with other pieces ( Figure 1.7).

Therefore, the purpose of sampling is to provide a means of evaluating the plausibility of several hypotheses about the structure of the population, through a limited number of observations and assuming that the structure of the population must be consistent with the structure of the sample. One immediate implication of this approach is that there are no sample size requirements in order to achieve representativeness.

Let us verify the truth of this statement and see if this approach to sampling is still valid in the extreme situation of a sample size of one. We know that with the first approach we would discard such a sample as non‐representative. Will we reach the same conclusion with the current approach?

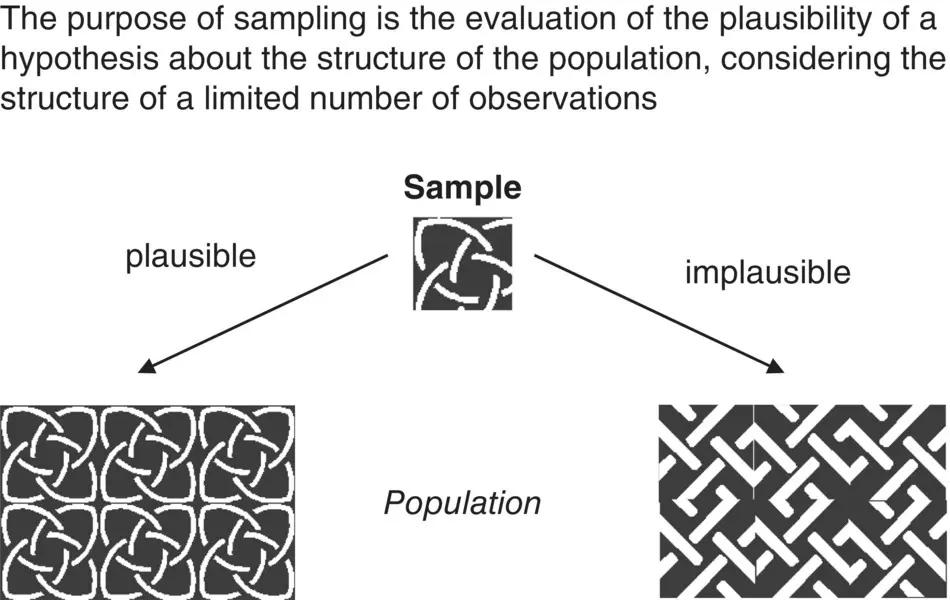
Figure 1.7 Modern view of the purpose of sampling. The purpose of sampling is the evaluation of the plausibility of a hypothesis about the structure of the population, considering the structure of a limited number of observations.

Imagine a swimming pool full of small balls. The color of the balls is the attribute we wish to study, and we know that it can take only one of two possible values: black and white. The problem at hand is to find the proportion of black balls in the population of balls inside the swimming pool. So we take a single ball out of the pool and let us say that the ball happened to be black ( Figure 1.8). What can we say about the proportion of black balls in the population?

We could start by saying that it is perfectly possible that the population consists 100% of black balls. We could also say that it is also quite plausible that the proportion of black balls is, say, 80% because then it would be quite natural that, by taking a single ball at random from the pool, we would get a black ball. However, if the proportion of black balls in the population is very small, say less than 5%, we would expect to get a white ball, rather than a black ball. In other words, a sample made up of a black ball is not very consistent with the hypothesis of a population with less than 5% of black balls. On the other hand, if the proportion of black balls in the population is between 5 and 100%, the result of the sampling is quite plausible. Consequently, we would conclude that the sample was consistent with a proportion of black balls in the swimming pool between 5 and 100%. The inference we would make from that sample would be to estimate as such the proportion of black balls, with a high degree of confidence.

One might say that this whole thing is nonsense, because such a conclusion is completely worthless. Of course it is, but that is because we did not bother spending a lot of effort in doing the study. If we wanted a more interesting conclusion, we would have to work harder and collect some more information about the population. That is, we would have to make some more observations to increase the sample size.

Before going into this, think for a moment about the previous study. There are three important things to note. First, this approach to sampling still works in the extreme situation of a sample size of one, while that is not true for the classical approach. Second, the conclusion was correct (remember, it was said that one was very confident that the proportion of black balls in the population was a number between 5 and 100%). The problem with the conclusion, better said with the study, was that it lacked precision. Third, the inference procedure described here is valid only for random samples of the population, otherwise the conclusions may be completely wrong. Suppose that the proportion of black balls in the population is minimal, but because their color attracts our attention, if we looked at the balls before getting our sample, we were much more likely to select a flashy black ball than a boring white one. We would then make the same reasoning as before and reach the same conclusion, but we would be completely wrong because the sample was biasedtoward the black balls.