Mickael Launay - It All Adds Up

According to one of the many stories put about on the subject, Thales was particularly absent-minded: he is said to have been a prime example from an age-old tradition of scatter-brained scholars. One tale reports that one night he was seen to fall into a well while roaming with his nose in the air observing the stars. Another tells us that he died aged almost eighty while attending a sporting event: so wrapped up did he become in the spectacle that he forgot to eat and drink.

His scientific prowess is also the subject of singular tales. Thales is viewed as the first person to have correctly predicted a solar eclipse. This one took place in the middle of a battle between the Medes and the Lydians, on the banks of the Halys River in the west of what is now Turkey. When night intervened in broad daylight, the warriors saw it as a message from the gods, and decided at once to make peace. Nowadays, the prediction of eclipses or their reconstitution in the past has become child’s play for our astronomers. Thanks to them, we know that this eclipse took place on 28 May 584 BC, making the battle of Halys the oldest historical event that we are able to date with such accuracy.

Thales’ greatest success was achieved on a journey to Egypt. The story goes that the Pharaoh Amasis in person challenged him to measure the height of the Great Pyramid. Until then, the Egyptian scholars who had been consulted had failed to answer the question correctly. Thales not only met the challenge, but did so in an elegant way, using a particularly clever method. He planted a stick vertically in the ground and waited for the time of day when the length of its shadow was equal to its height. At that very same moment, he marked and then measured the shadow of the pyramid, which likewise must be equal to its height. That did the trick!

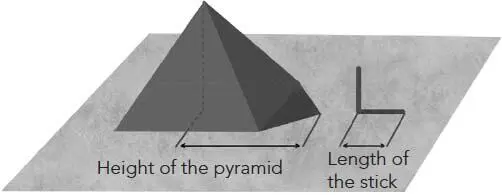
The story is certainly entertaining, but once again its historical truth is dubious. Moreover, as it is told, the anecdote is quite scornful of the Egyptian scholars of the period, although papyruses such as that copied by Ahmes show that these scholars knew perfectly well how to calculate the height of their pyramids more than a thousand years before Thales came on the scene. So where does the truth lie? Did Thales really measure the height of the pyramid? Was he the first to use the shadow method? And what if he had simply measured the height of an olive tree in front of his house in Miletus, and his disciples took it upon themselves to embroider the story after his death? We have to abide by the evidence, and we shall probably never have it.

Be that as it may, Thales’ geometry, on the other hand, is very real, and whether he applied it to the Great Pyramid or to an olive tree, the shadow method is no less appealing. This method represents a particular case of a property now known as Thales’ theorem. Several other mathematical results are also attributed to Thales: the circle is divided in two equal parts by any diameter (fig. 1); the angles at the base of an isosceles triangle are equal (fig. 2); the opposite angles produced at the point of intersection of two straight lines are equal (fig. 3); if the three vertices of a triangle lie on a circle and one side passes through the centre of this circle, then the triangle is a right-angled triangle (fig. 4). In fact, this last statement is sometimes also referred to as Thales’ theorem.

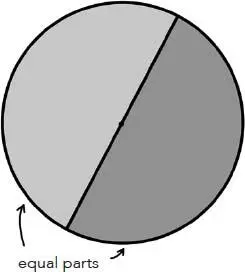
Fig. 1

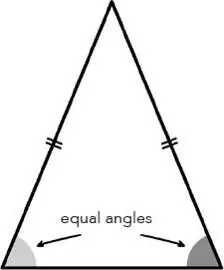
Fig. 2

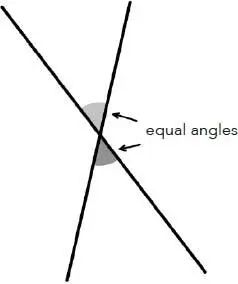
Fig. 3

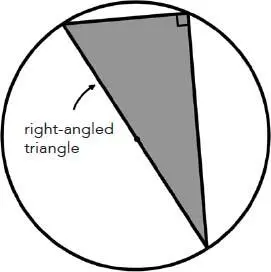
Fig. 4

I want to look at this strange word that is as fascinating as it is awesome: what is a theorem? Etymologically, the word comes from the Greek thea (contemplation) and horáō (to see), so a theorem would be a sort of observation on the world of mathematics, a fact that would have been noted, examined and then recorded by mathematicians. Theorems can be transmitted orally or in writing, and are similar to one’s grandmother’s recipes or to weather lore that has been tested over the generations and is confidently believed to be true. One swallow does not make a summer, bay leaves soothe rheumatism, and the 3-4-5 triangle has a right angle. These are things we believe to be true and that we keep in mind in order to use them when they are relevant.

According to this definition, the Mesopotamians, the Egyptians and the Chinese also stated theorems. However, beginning with Thales, the Greeks gave them a new dimension. For them, a theorem not only had to state a mathematical truth, but that truth must be formulated in the most general way possible, and accompanied by a proof of its validity.

Back to one of the properties attributed to Thales: that the diameter of a circle divides the circle into two equal parts. Such an assertion may seem disappointing coming from a scholar of Thales’ calibre. It seems self-evident; why did we have to wait until the sixth century BC for such a trivial assertion to be stated? There is no doubt that Egyptian and Babylonian scholars must have known that a long time beforehand.

Make no mistake. The audacious thing about that property attributed to Thales is not so much its content as its formulation. Thales dared to speak about a circle without saying precisely which one. In order to state the same rule, the Babylonians, Egyptians and Chinese would have used an example. Draw a circle of radius 3 and draw one of its diameters, they would have said, and this circle is divided into two equal parts by this diameter. And when one example did not suffice for an understanding of the rule, they would have given a second one, a third, and a fourth if necessary. They would have given as many examples as needed to enable readers to understand that they could repeat the same procedure on every circle they might meet. But the general assertion was never formulated.

Thales reached a milestone.

‘Take a circle, any one you like, I don’t need to know which. It may be enormous or tiny. Draw it in the horizontal, in the vertical or on an inclined plane, it doesn’t matter to me. I don’t care at all about your particular circle and how you have drawn it. However, I assert that its diameter divides it into two equal parts.’

With this operation, Thales definitively assigned the status of abstract mathematical objects to geometric figures. This step in thinking was similar to that taken 2,000 years earlier by the Mesopotamians when they considered numbers independently from the objects counted. A circle was no longer a figure drawn on the ground, on a tablet or on a papyrus. The circle became a fiction, an idea, an abstract ideal all of whose real representations are merely imperfect instances.

From that point on, mathematical truths were stated in a concise and general manner, independently of the various particular cases they covered. It is these statements that the Greeks then called theorems.

Thales had several disciples in Miletus. The two most famous were Anaximenes and Anaximander. Anaximander in turn had his own disciples, who included a certain Pythagoras, who would give his name to the most famous theorem of all time.