Michael Begon - Ecology

dynamic patterns: R and b

Equation 5.18also shares with other good models an ability to throw fresh light on the real world. Analysing the population dynamics generated by the equation, we can draw guarded conclusions about the dynamics of natural populations. The mathematical method by which this and similar equations can be examined is described by May (1975a), but the results of the analysis ( Figure 5.23) can be appreciated without dwelling on the analysis itself. Figure 5.23a sets out the conditions under which we get the various patterns of population growth and dynamics that Equation 5.18can generate. Figure 5.23b shows what these patterns are. Note first that the pattern of dynamics depends on two things: (i) b , the precise type of competition or density dependence; and (ii) R , the effective net reproductive rate (taking density‐independent mortality into account). By contrast, a determines not the pattern of fluctuation, but only the level about which any fluctuations occur.

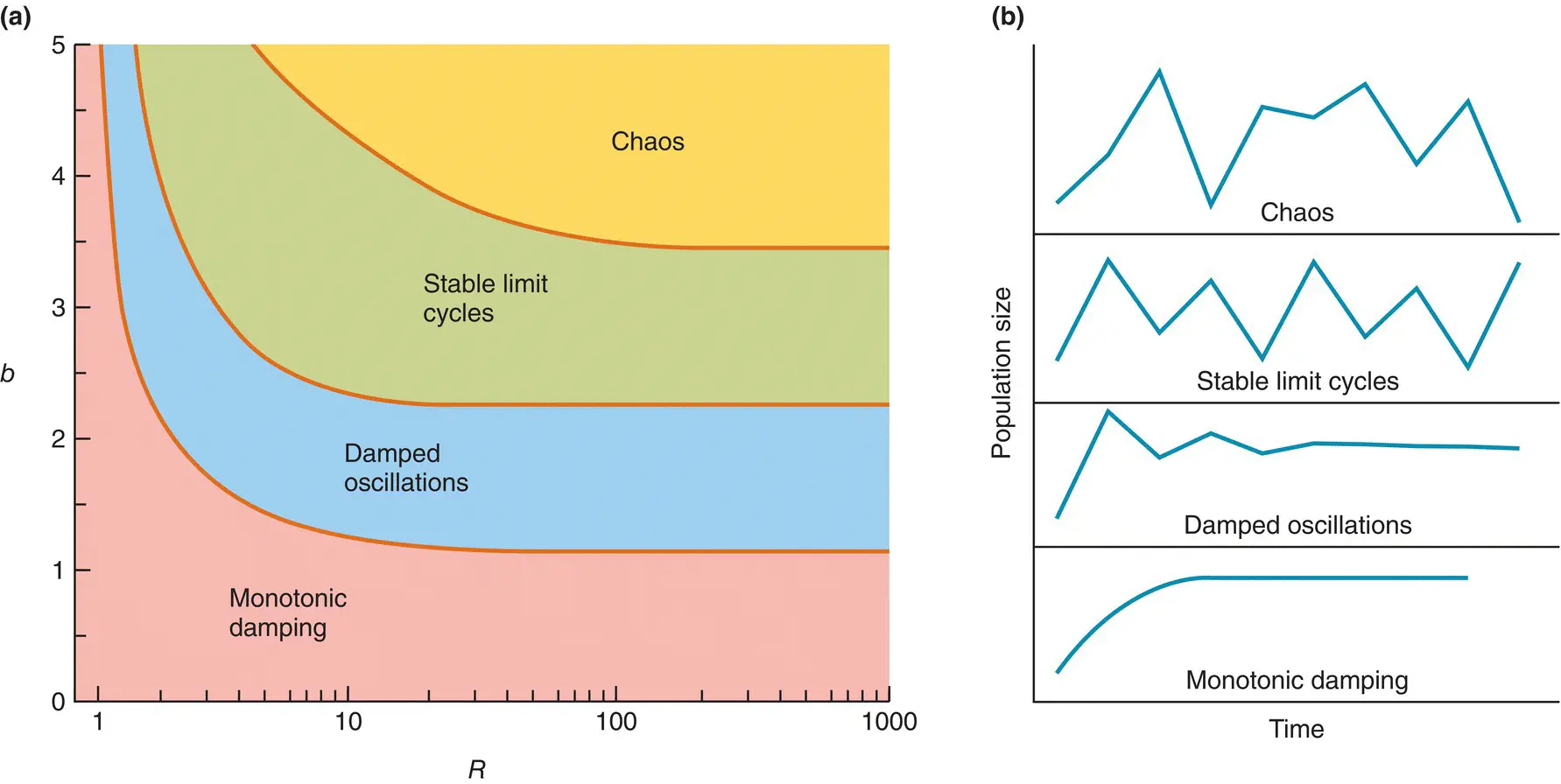
Figure 5.23 The range of population fluctuations generated by Equation 5.19 . (a) Reflecting the various possible combinations of b and R . (b) The patterns of those fluctuations.

Source : After May (1975a) and Bellows (1981).

As Figure 5.23a shows, low values of b and/or R lead to populations that approach their equilibrium size without fluctuating at all (‘monotonic damping’). This has already been hinted at in Figure 5.20a. There, a population behaving in conformity with Equation 5.12approached equilibrium directly, irrespective of the value of R . Equation 5.12is a special case of Equation 5.18in which b = 1 (perfect compensation). Figure 5.23a confirms that for b = 1, monotonic damping is the rule whatever the effective net reproductive rate.

As the values of b and/or R increase, the behaviour of the population changes first to damped oscillations gradually approaching equilibrium, and then to ‘stable limit cycles’ in which the population fluctuates around an equilibrium level, revisiting the same two, four or even more points time and time again. Finally, with large values of b and R , the population fluctuates in an apparently irregular and chaotic fashion.

Thus, a model built around a density‐dependent, supposedly regulatory process (intraspecific competition) can lead to a very wide range of population dynamics. If a model population has even a moderate fundamental net reproductive rate (and the ability to leave 100 (= R ) offspring in the next generation in a competition‐free environment is not unreasonable), and if it has a density‐dependent reaction which even moderately overcompensates, then far from being stable, it may fluctuate widely in numbers without the action of any extrinsic factor. The biological significance of this is the strong suggestion that even in an environment that is wholly constant and predictable, the intrinsic qualities of a population and the individuals within it may, by themselves, give rise to population dynamics with large and perhaps even chaotic fluctuations. The consequences of intraspecific competition are clearly not limited to ‘tightly controlled regulation’.

Two things are therefore clear. Firstly, time lags, high reproductive rates and overcompensating density dependence are capable (either alone or in combination) of producing all types of fluctuations in population density, without invoking any extrinsic cause. Secondly, and equally important, this has been made apparent by the analysis of mathematical models.

key characteristics of chaotic dynamics

In fact, the recognition that even simple ecological systems may contain the seeds of chaos led to chaos itself becoming a topic of interest amongst ecologists (Schaffer & Kot, 1986 ; Hastings et al ., 1993 ; Perry et al ., 2000). A detailed exposition of the nature of chaos is not appropriate here, but a few key points should be understood.

Firstly, the term ‘chaos’ may itself be misleading if it is taken to imply a fluctuation with absolutely no discernable pattern. Chaotic dynamics do not consist of a sequence of random numbers. On the contrary, there are tests (although they are not always easy to put into practice) designed to distinguish chaotic from random and other types of fluctuations. And since these patterns emerge from deterministic models (i.e. models with no random forces (stochasticity) incorporated), the term ‘deterministic chaos’ has been popularly used to describe them.

Secondly, fluctuations in chaotic ecological systems occur between definable upper and lower densities. Thus, in the model of intraspecific competition that we have discussed, the idea of ‘regulation’ has not been lost altogether, even in the chaotic region.

Third, however, unlike the behaviour of truly regulated systems, two similar population trajectories in a chaotic system will not tend to converge on (‘be attracted to’) the same equilibrium density or the same limit cycle (both of them ‘simple’ attractors). Rather, the behaviour of a chaotic system is governed by a ‘ strange attractor’. Initially very similar trajectories become exponentially less and less like one another over time: chaotic systems exhibit ‘extreme sensitivity to initial conditions’.

Hence, and finally, the long‐term future behaviour of a chaotic system is effectively impossible to predict, and prediction becomes increasingly inaccurate as one moves further into the future. Even if we appear to have seen the system in a particular state before – and know precisely what happened subsequently last time – tiny (perhaps immeasurable) initial differences will be magnified progressively, and past experience will become of increasingly little value.

beyond chaos

This altered perspective opened up by an appreciation of chaos led initially to an excited optimism, but as Bjørnstad (2015) explains, ecologists grew steadily more sceptical. There were occasional demonstrations of apparent chaos in artificial laboratory environments (Costantino et al ., 1997), but the unlikelihood of natural systems being devoid of random forces and having very few interacting elements, combined with technical difficulties in detecting the signature of chaos in real datasets (Bjørnstad & Grenfell, 2001), led to questions of how often, if ever, ecological systems are chaotic, and whether, practically, we could detect chaos in nature even if it existed. The fashion for studying chaos has largely passed. Nonetheless, the altered perspective – that unpredictability may be inherent in ecological systems without the involvement of major perturbations from outside the system – has been far more enduring. Ecology must aim to become a predictive science. Chaotic systems, if they exist, would set us some of the sternest challenges in prediction. But unanticipated shifts in dynamics from one pattern to another, and the transient dynamics that may link them, set similar challenges that continue to be taken up. We return to these in Chapters 14and 17.

The models described so far have all been ‘deterministic’ models, that is, once the parameter values of the model have been specified (for example, Equation 5.7with N t= 10, R = 1.1) the outcome is definite, or ‘determined’. Whenever that model is run with those values, the outcome is the same: after one time step, for example, there will be 11 individuals in the population. But the real world is not like that. The most that we could say of any population would be that, over each time step, there is a certain probability that there will be no births, a probability that there will be one birth, a probability that there will be no deaths, and so on – such that typically, or on average, 10 individuals will become 11 individuals over the course of a time step. The actual outcome, though, would reflect the consequences of those probabilities playing out: sometimes 11 individuals, but sometimes 10, or 12, or more rarely 9, or 13, etc. Stochastic population models incorporate these probabilistic processes. They are therefore more realistic, but also more unwieldy, more difficult to analyse, and for the non‐specialist, more difficult to understand. Along related lines, individual‐based models deal with these stochastic processes by explicitly acknowledging each individual in a population and giving those individuals their own chances of being born, dying, and in more complex models, moving or growing, and so on (Black & McKane, 2012).