Michael Begon - Ecology

Until now, we have focused on what happens to the whole population or the average individual within it. Different individuals, however, may respond to intraspecific competition in very different ways. For example, when larval salamanders ( Ambystoma tigrinum nebulosum ) were competed amongst one another in groups, the sizes of the largest surviving larvae were no different from those reared alone ( P = 0.42) but the smallest larvae were much smaller ( P < 0.0001) (Ziemba & Collins, 1999). Similarly, the overwinter survival of red deer calves, Cervus elaphus , in the resource‐limited population on the island of Rhum, Scotland, declined sharply as the population became more crowded, but those that were smallest at birth were by far the most likely to die (Clutton‐Brock et al ., 1987). The effects of competition are far from being the same for every individual. Weak competitors may make only a small contribution to the next generation, or no contribution at all. Strong competitors may have their contribution only negligibly affected.

What effect does this have at the population level? Figure 5.26shows the results of a classic experiment in which flax ( Linum usitatissimum ) was sown at three densities, and harvested at three stages of development, recording the weight of each plant individually. This made it possible to monitor the effects of increasing amounts of competition not only as a result of variations in initial density, but also as a result of plant growth (between the first and the last harvests). When intraspecific competition was at its least intense (at the lowest sowing density after only two weeks’ growth) the individual plant weights were distributed symmetrically about the mean. When competition was at its most intense, however, the distribution was strongly skewed to the left: there were many very small individuals and a few large ones. As the intensity of competition gradually increased, the degree of skewness increased as well. Something very similar seems to be happening with the data in Figure 5.27for cod ( Gadus morhua ) living off the coast of Norway. At higher densities (and presumably greater intensities of competition) size decreased but the skewness in the distribution of sizes increased.

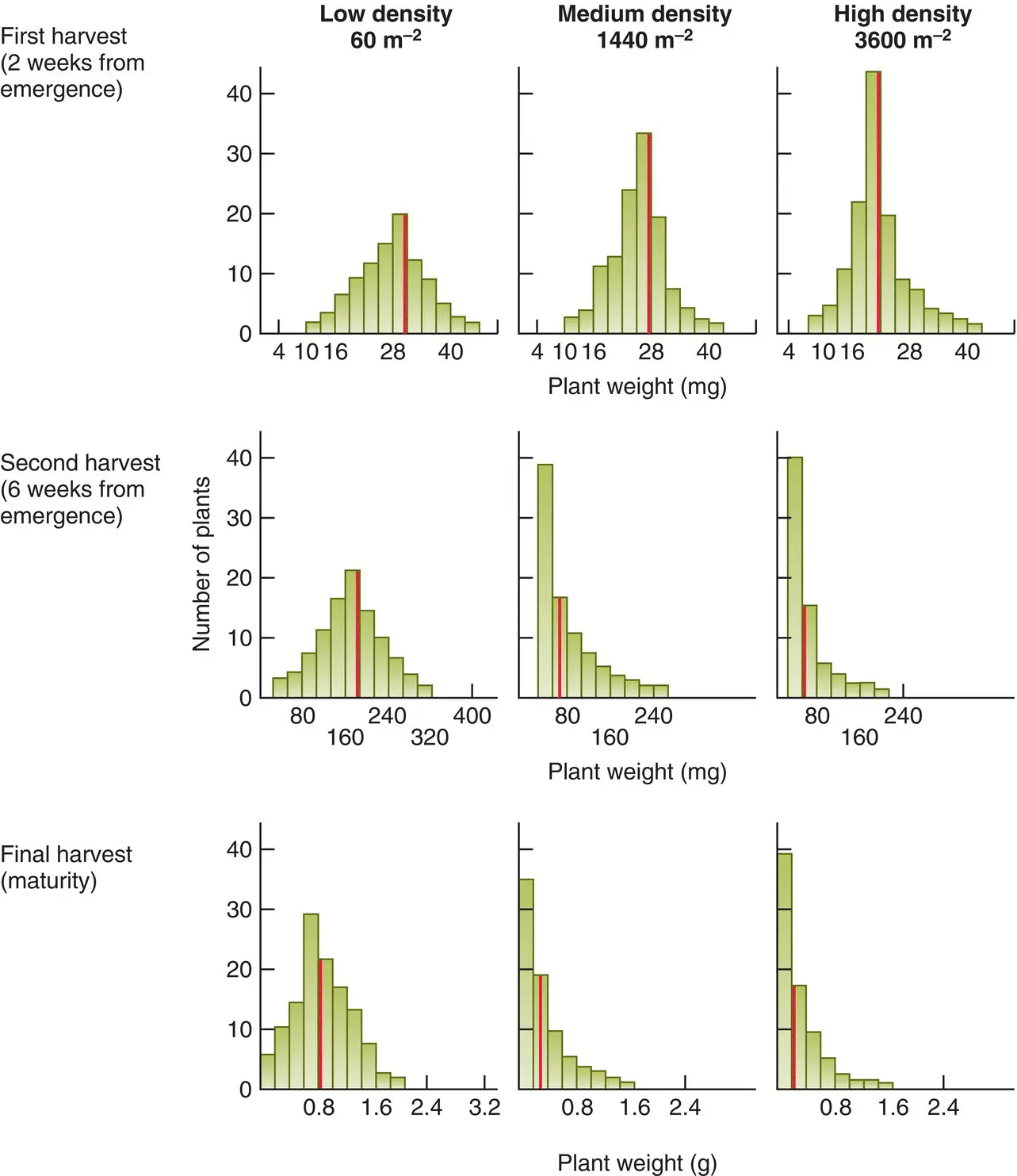
Figure 5.26 Intraspecific competition increases the skewing in the distribution of plant weights.Frequency distributions of individual plant weights in populations of flax ( Linum usitatissimum ), sown at three densities and harvested at three ages. The red bar is the mean weight.

Source : After Obeid et al . (1967).

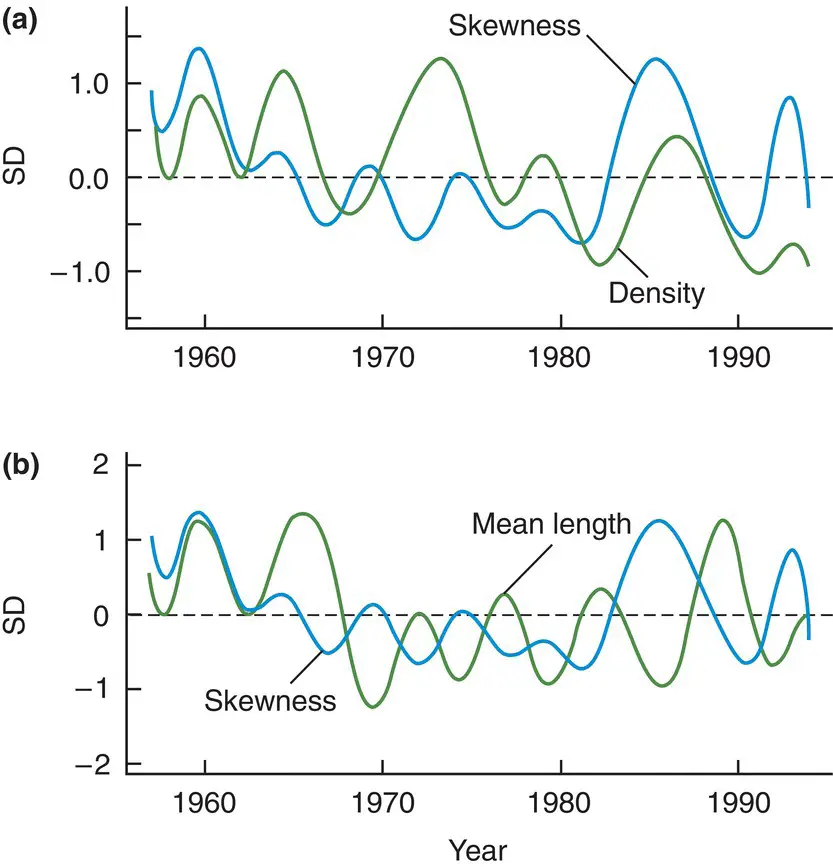
Figure 5.27 Intraspecific competition increases the skewing in the distribution of cod lengths but decreases mean length.(a) Values of density and of skewness in the frequency distribution of lengths, both expressed as standard deviations from mean values, for the years 1957–94 for cod ( Gadus morhua ) from the Skagerrak, off the coast of Norway. (b) Similar patterns for skewness and mean length. Despite marked fluctuations from year to year, much of it the result of variations in weather, when density rose, that is, when competition was most intense, skewness tended also to rise ( r = 0.58, P < 0.01) but mean length tended to decline ( r = −0.45, P < 0.05).

Source : After Lekve et al . (2002).

the inadequacy of the average

Skewness aside, we can say more generally that increased competition tends to increase the degree of size inequality within a population, at least initially (Weiner, 1990). Characterising a population by an arbitrary ‘average’ individual can therefore be very misleading under such circumstances, and can divert attention from the fact that intraspecific competition is a force affecting individuals, even though its effects may often be detected in whole populations.

The processes by which these size inequalities may be generated, and also ultimately diminished, are illustrated by a study of competition in two separate species of large brown seaweed, Laminaria digitata and Fucus serratus , off the Isle of Man, UK, reared at a range of densities, from 650 to 5156 plants per m 2( Figure 5.28). We can see, firstly, that for all populations there was, for a large part of the experiment, a marked tendency for size inequality to increase ( Figure 5.28a). The Gini coefficient (a measure of inequality originally developed by economists to capture inequalities in wealth), applied to frond (leaf) lengths, increased steadily as the plants grew, that is, as mean mass increased and competition intensified. However, for many of the populations, as the plants grew further still, the Gini coefficient declined again.

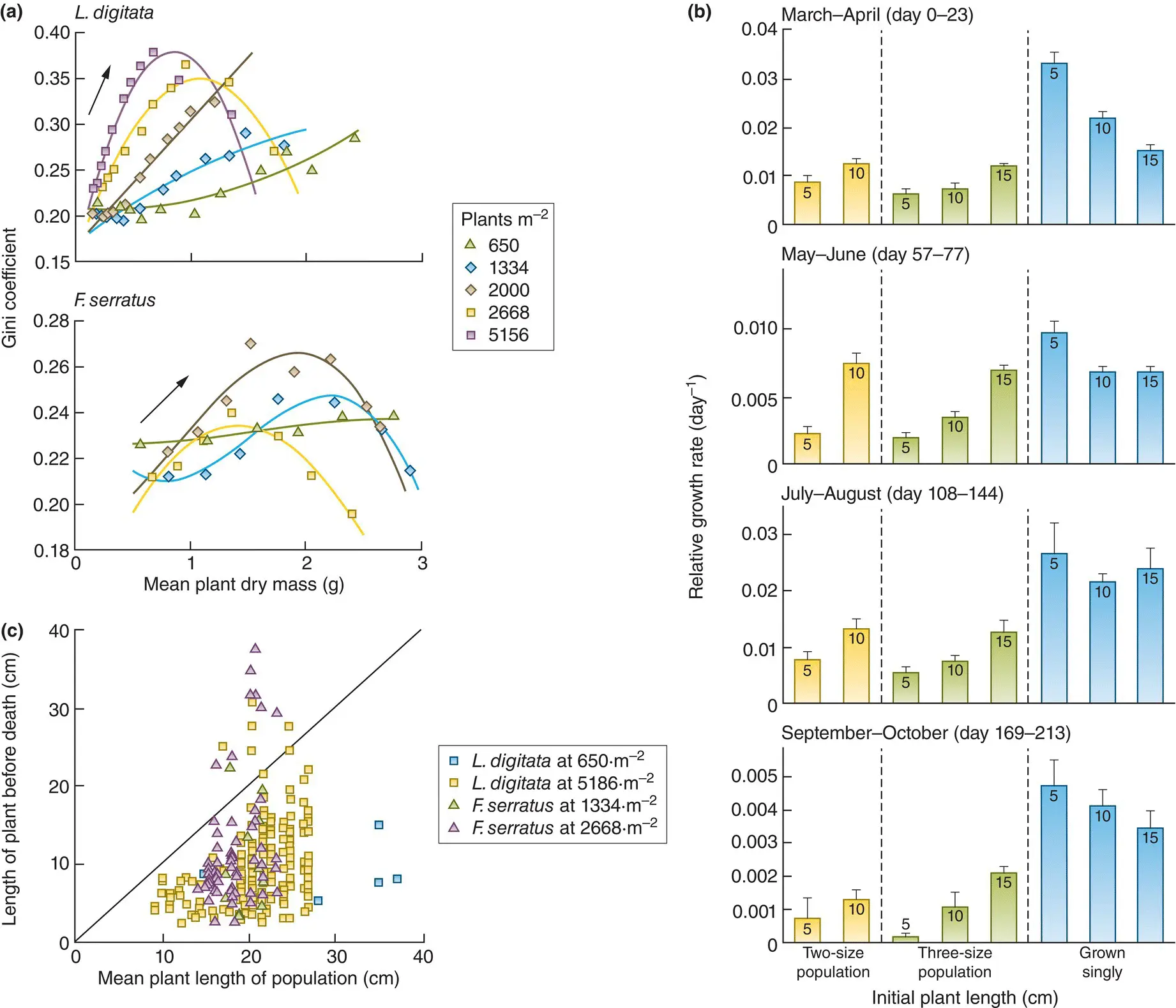
Figure 5.28 Size inequalities first increase then decrease in competing populations of seaweeds.(a) The effect of density on the relationship between inequality of plant frond lengths (measured by Gini coefficients) and mean plant mass in populations of Laminaria digitata (above) and Fucus serratus (below) at the range of densities indicated. Data are means ( n = 4). Curved lines are fitted by polynomial functions to indicate the general pattern of change between variables. Arrows indicate the direction of the time sequence. (b) The relative growth rates of L. digitata plants grown singly and in populations consisting of two or three sizes of plants over four selected time periods. Data are means of n = 6 singly grown plants and n = 3 population means for portions of populations. Bars are numbered to indicate initial plant size (in cm). Bars are SEs. (c) The frond length of L. digitata and F. serratus plants at the sample time before death, plotted against the population mean frond length at that time. Two densities for each species are plotted to demonstrate the generality of the relationships. The diagonal line represents the condition where the length of the dying plants equals the population mean plant length.

Source : After Creed et al . (1998).

The process driving the initial increases in inequality is illustrated in Figure 5.28b. This shows data on the relative growth rates of L. digitata plants of different initial lengths (5 cm, 10 cm and 15 cm). Relative growth rates measure changes in mass relative to initial mass, which makes sense since without this correction, large plants would almost inevitably grow faster than small ones. The plants were combined in populations of different size‐composition but at a high density (7619 plants m –2) where competition would have been intense. Plants were also grown in isolation. When grown singly, the smallest plants grew fastest, at least initially. However, as soon as they were combined, either with two or three size‐classes together, the growth‐rate differentials were reversed, with the smallest plants growing least and the largest most. Indeed, in some cases, the growth of the larger plants was barely affected by competition. Size inequality increased, therefore, because plants that were smaller initially were more affected by their neighbours. Small initial differences were transformed by competition into much larger differences over time. Competition amongst the seaweeds was therefore asymmetric: there was a hierarchy. It seems that the larger plants pre‐empted or ‘captured’ space and resources, and subsequently were little affected by intraspecific competition, while the smaller plants were being starved of these resources. Berntson and Wayne (2000) provide a rare empirical confirmation of such size‐uptake relationships for developing stands of birch seedlings ( Betula alleghaniensis ).