Table 2.6 Calculation of the variance and standard deviation for 16 subjects from the corn size data.
|
Corn |
|
|
Square of |
|
|
size |
|
Differences |
differences |
|
| Subject |
( mm ) |
Mean |
from mean |
from mean |
|
| ( i ) |
( x i) |
( 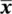 ) ) |
( 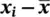 ) ) |
( 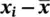 ) 2 ) 2 |
|
| 1 |
1 |
3.625 |
−2.625 |
6.891 |
|
| 2 |
2 |
3.625 |
−1.625 |
2.641 |
|
| 3 |
2 |
3.625 |
−1.625 |
2.641 |
|
| 4 |
2 |
3.625 |
−1.625 |
2.641 |
|
| 5 |
2 |
3.625 |
−1.625 |
2.641 |
|
| 6 |
2 |
3.625 |
−1.625 |
2.641 |
|
| 7 |
3 |
3.625 |
−0.625 |
0.391 |
|
| 8 |
3 |
3.625 |
−0.625 |
0.391 |
|
| 9 |
3 |
3.625 |
−0.625 |
0.391 |
|
| 10 |
3 |
3.625 |
−0.625 |
0.391 |
|
| 11 |
4 |
3.625 |
0.375 |
0.141 |
|
| 12 |
4 |
3.625 |
0.375 |
0.141 |
|
| 13 |
5 |
3.625 |
1.375 |
1.891 |
|
| 14 |
6 |
3.625 |
2.375 |
5.641 |
|
| 15 |
6 |
3.625 |
2.375 |
5.641 |
|
| 16 |
10 |
3.625 |
6.375 |
40.641 |
|
| Total |
58 |
|
0.000 |
75.756 |
|
|
n |
Mean |
df = n−1 |
Variance |
SD |
|
16 |
3.625 mm |
15 |
5.050 mm 2 |
2.247 mm |
Why is the Standard Deviation Useful?
From the corn plaster trial data, the mean and standard deviation of the baseline corn size of the 200 trial patients are 3.8 and 1.8 mm respectively (two baseline sizes were missing). It turns out in many situations that about 95% of observations will be within two standard deviations of the mean. This is known as a reference interval or reference range and it is this characteristic of the standard deviation which makes it so useful. It holds for a large number of measurements commonly made in medicine. In particular it holds for data that follow a Normal distribution (see Chapter 4).
For example, the Association for Clinical Biochemistry and Laboratory Medicine gives a number of reference ranges in biochemistry such as for serum potassium of 3.5–5.3 mmol l −1(labtestsonline 2019, https://labtestsonline.org.uk/articles/laboratory‐test‐reference‐ranges). This means in a normal, health population we would expect 19 out of 20 people to have serum potassium levels within these limits. For the corn plaster example, we would expect the majority of corns will be sized between 3.8–1.96 × 1.8 to 3.8 + 1.96 × 1.8 or 0.2 and 7.4 mm. Table 2.7shows that there are 10 patients out of 200 (or 5%) who have a corn size above 7.4 mm and none below 1 mm; thus 95% of the observations in the data lie with two standard deviations of the mean.
Table 2.7 Frequency distribution the size of the corn, in mm, at baseline for 200 patients with corns who were recruited to a randomised control trial of the effectiveness of salicylic acid plasters compared with ‘usual’ scalpel debridement for the treatment of corns
( Source: data from Farndon et al. 2013).
| Size of corn at baseline (mm) |
Frequency |
Percentage |
Cumulative percentage |
| 1 to <2 |
6 |
3.0 |
3.0 |
| 2 to <3 |
39 |
19.5 |
22.5 |
| 3 to <4 |
52 |
26.0 |
48.5 |
| 4 to <5 |
42 |
21.0 |
69.5 |
| 5 to <6 |
38 |
19.0 |
88.5 |
| 6 to <7 |
10 |
5.0 |
93.5 |
| 7 to <8 |
3 |
1.5 |
95.0 |
| 8 to <9 |
5 |
2.5 |
97.5 |
| 9 to <10 |
1 |
0.5 |
98.0 |
| 10 to <11 |
4 |
2.0 |
100 |
| Total |
200 |
100 |
|
As we have noted, standard deviation is often abbreviated to SD in the medical literature. Sometimes for emphasis we will denote it by SD( x ), where the bracketed term x is included for a reason to be introduced later.
Means and medians convey different impressions of the location of data, and one cannot give a prescription as to which is preferable; often both give useful information. If the distribution is symmetric, then in general the mean is the better summary statistic, and if it is skewed then the median is less influenced by the tails. If the data are skewed, then the median will reflect a ‘typical’ individual better. For example, if in a country median income is £20 000 and mean income is £24 000, most people will relate better to the former number.
It is sometimes stated, incorrectly, that the mean cannot be used with binary, or ordered categorical data but, as we have noted before, if binary data are scored 0/1 then the mean is simply the proportion of 1s. If the data are ordered categorical, then again the data can be scored, say 1, 2, 3, etc. and a mean calculated. This can often give more useful information than a median for such data, but should be used with care, because of the implicit assumption that the change from score 1 to 2, say, has the same meaning (value) as the change from score 2 to 3, and so on.
2.5 Displaying Continuous Data
A picture is worth a thousand words, or numbers, and there is no better way of getting a ‘feel’ for the data than to display them in a figure or graph. The general principle should be to convey as much information as possible in the figure, with the constraint that the reader is not overwhelmed by too much detail.
The simplest method of conveying as much information as possible is to show all of the data and this can be conveniently carried out using a dot plot. It is also useful for showing the distributions in two or more groups side by side.
Example – Dot Plot – Baseline Corn Size
The data on corn size and treatment group (corn plaster or scalpel) are shown in Figure 2.5as a dot plot. This method of presentation retains the individual subject values and clearly demonstrates any similarities or differences between the groups in a readily appreciated manner. An additional advantage is that any outliers will be detected by such a plot. However, such presentation is not usually practical with large numbers of subjects in each group because the dots will obscure the details of the distribution. Figure 2.5shows that the two randomised groups had similar distributions of corn sizes at baseline.
Читать дальше

 )
)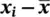 )
)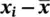 ) 2
) 2










