Example – Calculation of the Range – Corn Size Data
The range for the corn size data is 1 to 10 mm or described by a single number 10 −1 = 9 mm.
Quartiles and the Interquartile Range
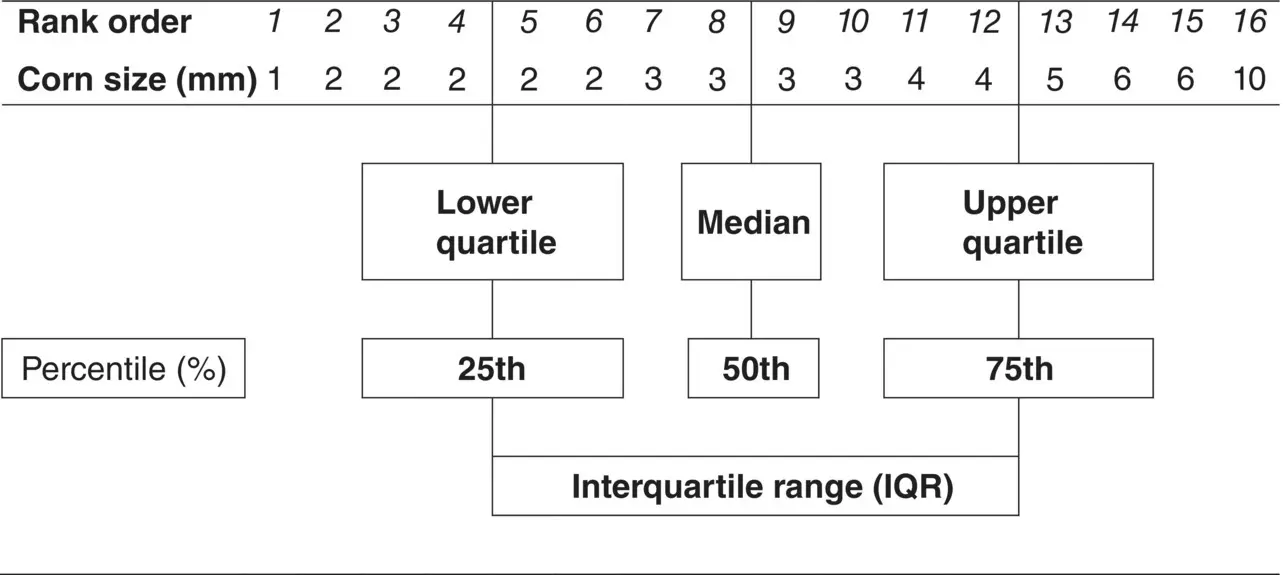
The quartiles, namely the lower quartile, the median and the upper quartile, divide the data into four equal parts using three cut‐points; that is there will be approximately equal numbers of observations in the four sections (and exactly equal if the sample size is divisible by four and the measures are all distinct). The quartiles are calculated in a similar way to the median; first order the data and then count the appropriate number from the bottom. The lower quartile is found by ranking the data and then taking the value below which 25% of the data sit. The upper quartile is the value above which the top 25% of the data points sit. The interquartile range is a useful measure of variability and is the range of values that includes the middle 50% of observations and is given by the difference between the lower and upper quartiles. The interquartile range is not vulnerable to outliers, and whatever the distribution of the data, we know that 50% of them lie within the interquartile range.
The median and quartiles are example of percentiles – points which divide the distribution of the data set into percentages above or below a certain value. A percentile (or a centile) is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations fall. For example, the 20th percentile is the value (or score) below which 20% of the observations may be found. The median is the 50th percentile, the lower quartile is the 25th percentile and the upper quartile is the 75th percentile. With enough data any percentile can be calculated from continuous data.
Example – Calculation of the Range, Quartiles, and Inter‐Quartile Range – Corn Size Data
Suppose, as in Table 2.5, we had the 16 corn sizes in millimetres arranged in increasing order (from smallest to largest) from the Farndon et al. (2013) study. The median is the average of the eighth and ninth ordered observations (3 + 3)/2 = 3 mm. The first or bottom or lower half of the data has eight observations; so the cut‐point for the first or lower quartile is the observation that splits the eight lowest ranked observations into two halves again, that is, four observations in each ‘half’. Thus, the lower quartile lies somewhere between the fourth and fifth ordered observations. When the quartile lies between two observations the easiest option is to take the mean of the two observations (although there are more complicated methods). So the lower quartile is (2 + 2)/2 = 2 mm.
Similarly, the upper quartile is calculated from the top half of the data (i.e. the observations with the largest values). The second or top or upper half of the data has eight observations; so again the cut‐point for the upper quartile is the observation that splits the eight highest ranked observations (ordered observations 9–16 into two halves again, (i.e. four observations in each ‘half’). Thus, the upper quartile lies somewhere between the 12th and 13th ordered observations. Since the quartile lies between two observations the easiest option is to take the mean of the two observations. Therefore, the upper quartile is (4 + 5)/2 = 4.5 mm. So, the interquartile range (IQR), for the corn size data, is from 2.0 to 4.5 mm; or a single number 2.5 mm.
Standard Deviation and Variance
A third measure of the amount of spread or variability in a data set is the standard deviation. It is based on the idea of averaging the distance each value is away from the sample mean, 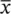 . For an individual with an observed value x ithe distance from the mean is
. For an individual with an observed value x ithe distance from the mean is 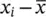 . With n such observations we have a set of n such differences, one for each individual. The sum of these differences,
. With n such observations we have a set of n such differences, one for each individual. The sum of these differences, 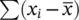 is always zero. However, if we square the distances before we sum them we get a positive quantity. This sum is then divided by ( n −1) and thus gives an average measure for the deviation from the mean. This quantity is called the variance and is defined as:
is always zero. However, if we square the distances before we sum them we get a positive quantity. This sum is then divided by ( n −1) and thus gives an average measure for the deviation from the mean. This quantity is called the variance and is defined as:
Table 2.5 Calculating the median, quartiles, and interquartile range for the corn size data.
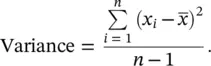
The variance is expressed in square units and so is not a suitable measure for describing variability because it is not in the same units as the raw data. The solution is to take the square root of the variance to return to the original units. This gives us the standard deviation (usually abbreviated to SD or s ) defined as:
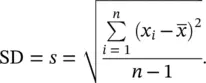
Examining this expression it can be seen that if all the x 's were the same, then they would all equal 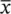 and so s would be zero. If the x 's were widely scattered about
and so s would be zero. If the x 's were widely scattered about  , then s would be large. In this way s reflects the variability in the data.
, then s would be large. In this way s reflects the variability in the data.
Illustrative Example – Calculation of the Standard Deviation – Foot Corn Size
The calculations to work out the standard deviation for the 16 corn sizes are given in Table 2.6.
A convenient method of removing the negative signs is by squaring the deviations, which is given in the next column, which is then summed to get 75.756 mm 2. Note that the majority of this sum (54%) is contributed by one observation, the value of 10 mm from subject 16, which is the observation furthest from the mean. This illustrates that much of the value of an SD is derived from the outlying observations. (The standard deviation is vulnerable to outliers, so if the 10 was replaced by 100 we would get a very different result.) We now need to find the average squared deviation. Common sense would suggest dividing by n , but it turns out that this actually gives an estimate of the population variance, which is too small. This is because we use the estimated mean 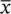 in the calculation in place of the true population mean. In fact, we seldom know the population mean so there is little choice but for us to use its estimated value,
in the calculation in place of the true population mean. In fact, we seldom know the population mean so there is little choice but for us to use its estimated value, 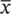 , in the calculation. The consequence is that it is then better to divide by what are known as the degrees of freedom, which in this case is n −1, to obtain the SD.
, in the calculation. The consequence is that it is then better to divide by what are known as the degrees of freedom, which in this case is n −1, to obtain the SD.
Читать дальше

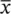 . For an individual with an observed value x ithe distance from the mean is
. For an individual with an observed value x ithe distance from the mean is 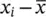 . With n such observations we have a set of n such differences, one for each individual. The sum of these differences,
. With n such observations we have a set of n such differences, one for each individual. The sum of these differences, 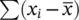 is always zero. However, if we square the distances before we sum them we get a positive quantity. This sum is then divided by ( n −1) and thus gives an average measure for the deviation from the mean. This quantity is called the variance and is defined as:
is always zero. However, if we square the distances before we sum them we get a positive quantity. This sum is then divided by ( n −1) and thus gives an average measure for the deviation from the mean. This quantity is called the variance and is defined as:
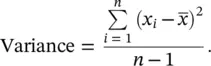
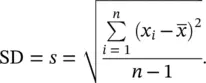
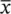 and so s would be zero. If the x 's were widely scattered about
and so s would be zero. If the x 's were widely scattered about  , then s would be large. In this way s reflects the variability in the data.
, then s would be large. In this way s reflects the variability in the data.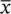 in the calculation in place of the true population mean. In fact, we seldom know the population mean so there is little choice but for us to use its estimated value,
in the calculation in place of the true population mean. In fact, we seldom know the population mean so there is little choice but for us to use its estimated value, 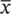 , in the calculation. The consequence is that it is then better to divide by what are known as the degrees of freedom, which in this case is n −1, to obtain the SD.
, in the calculation. The consequence is that it is then better to divide by what are known as the degrees of freedom, which in this case is n −1, to obtain the SD.










